Dedukcja lokalna – na przykładzie
Twierdzenie Talesa dowieść można bez trudu...
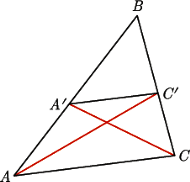
To twierdzenie (i jego dowód) to Twierdzenie 2 z szóstej księgi Elementów Euklidesa.
Mamy udowodnić
Twierdzenie. Jeśli prosta równoległa do jego boku 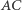 przecina trójkąt
przecina trójkąt 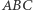 w punktach
w punktach 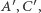 to
to 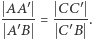
Oto ten dowód.

Pierwsza i piąta równość bierze się stąd, że mamy trójkąty o podstawach na jednej prostej i wspólnym trzecim wierzchołku, druga i czwarta to tylko permutacja wierzchołków w każdym trójkącie z osobna. Kluczowa jest równość trzecia: mianownik jest ten sam, a w liczniku mamy trójkąty o podstawie 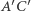 - mają one równe wysokości, bo
- mają one równe wysokości, bo 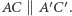
Z tak sformułowanego twierdzenia Talesa wynikają już dość mechanicznie wszystkie jego inne postacie, w tym ta, nazywana w szkole twierdzeniem odwrotnym.
Fundamentalista zakrzyknie: tu jest wykorzystany wzór na pole trójkąta - a skąd go wziąć?
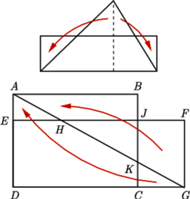
Proszę bardzo, oto dowód, że każdy trójkąt da się pociąć na kawałki, z których ułoży się kwadrat - nietrudno się zorientować, że jego pole (nawet fundamentaliści chyba zgodzą się co do wartości pola kwadratu) będzie takie samo dla trójkątów, których tradycyjnie obliczone pola uważamy za równe.
Trójkąt tniemy na trzy kawałki, które przez przemieszczenie dają prostokąt. Już Starożytni wiedzieli jak, ale dopiero dziewiętnastowieczni Farkas Bolyai i Paul Gerwien nadali swoje imię pocięciu prostokąta tak, by uzyskać dowolny inny prostokąt o tym samym polu - w szczególności więc kwadrat.
Aby uzyskać przedstawione na rysunku przesunięcia trójkąta 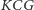 o wektor
o wektor 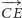 na
na 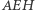 i trójkąta
i trójkąta 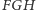 o wektor
o wektor 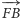 na
na 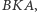 trzeba wykazać, że oba te wektory są równoległe do
trzeba wykazać, że oba te wektory są równoległe do 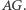 Założona równość pól to
Założona równość pól to 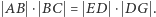 Z niej Czytelnik Niedowierzający wyprowadzi bez trudu równość
Z niej Czytelnik Niedowierzający wyprowadzi bez trudu równość

która na mocy twierdzenia Talesa (właśnie w tej odwrotnej postaci) daje żądane równoległości.
To co - mamy błędne koło? Bynajmniej: twierdzenie Bolyaia-Gerwiena i twierdzenie Talesa są równoważne... no właśnie: na jakim gruncie?
I tu dotykamy rzeczy najbardziej istotnej dla działań matematyków. Faktycznie nie posługują się oni dowodzeniem twierdzeń, wychodząc od aksjomatyki, ale od pewnego, zawsze bogatego zbioru faktów, o których tak oni, jak ich koledzy po fachu, są przekonani, że to już ktoś kiedyś udowodnił. Oni dokonują po prostu kolejnego kroku na drodze matematycznego poznania, taki krok nazywa się dedukcją lokalną. Takiego sposobu dowodzenia wymaga się (tu i ówdzie zapewne) od uczniów w szkole i żąda od olimpijczyków.
Pełnej dedukcji z aksjomatów w żadnej sensownej gałęzi matematyki nie wymaga się od uprawiających ją na tej samej zasadzie, jak nie wymaga się od programisty pisania instrukcji dla komputera przez wystukiwanie samych jedynek i zer.
Przykład obrałem z geometrii dlatego, że w jej przypadku przekonanie o istnieniu dającej się używać przez ogół aksjomatyki jest dość powszechne, a na dodatek utwierdzane przez czczone przez uczonych (nie tylko matematyków) Elementy Euklidesa - genialne w swoich rozumowaniach, ale niespełniające naszych dzisiejszych wyobrażeń o formalnych dowodach.