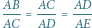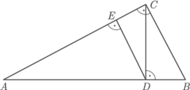
Rys. 1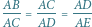

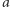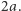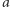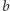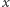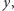W języku arytmetyki będzie to brzmiało: znajdź dwie średnie proporcjonalne dla i Dwie średnie proporcjonalne dla i to takie liczby i że

Przykład geometrycznej realizacji jest na rysunku 1

Podwojenie sześcianu byłoby zrealizowane, gdybyśmy umieli narysować taką konstrukcję dla 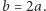Wtedy bowiem

Archytas z Tarentu postanowił tę konstrukcję zrealizować, posługując się metodą nazwaną później analizą Starożytnych. Polega ona na przyjęciu założenia, że mamy żądany obiekt i badaniu jego jak najliczniejszych własności w nadziei na to, że może któreś ze znalezionych pozwolą ten obiekt skonstruować.

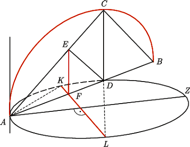
Rys. 2

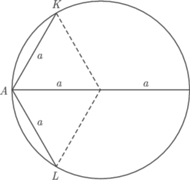
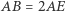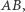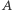Pomysł Archytasa polegał na wskazaniu żądanych punktów w przecięciu trzech znanych powierzchni, czyli nie na płaszczyźnie, lecz w przestrzeni. W tym celu wyposażył rysunek 1 wykonany dla w półokrąg o średnicy czyli o promieniu Na płaszczyźnie narysował okrąg o promieniu i na nim, prostopadle do płaszczyzny umieścił figurę z rysunku 1 w taki sposób, by punkty i 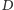znajdowały się na 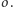Oznaczmy jeszcze przez 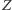przeciwny do 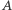koniec średnicy Następnie z opuśćmy wysokość na otrzymując 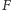i przez ten punkt poprowadźmy prostopadłą do 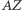- jej przecięcia z to 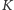i 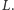Zauważmy, że

Pierwsza równość wynika z tego, że w trójkącie prostokątnym 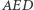wysokość jest średnią geometryczną odcinków, na jakie dzieli przyprostokątną. Druga równość wynika z podobieństwa trójkątów 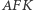i 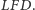Nieoczekiwany wniosek to fakt, że trójkąt 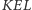okazuje się prostokątny (jako, że jego wysokość jest średnią geometryczną odcinków na jakie dzieli ).

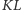Rys. 3

Wyobraźmy sobie teraz okrąg opisany na 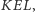którego średnicą jest Leży on w płaszczyźnie prostopadłej do 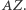Zatem wszystkie z punktów 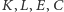leżą na powierzchni stożka o osi 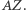Kąt pomiędzy osią a tworzącymi stożka t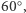o bo 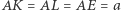(patrz rysunek 3).

Rys. 4

Koniec rozumowania Archytasa jest taki. Punkt można zlokalizować, zauważając, że poza tym, iż leży on na stożku, leży on także na walcu o tworzących przecinających okrąg i prostopadłych do jego płaszczyzny oraz na "torusie bez dziurki" - tę ostatnią powierzchnię otrzymamy, uzupełniając półokrąg opisany na do okręgu i obracając go dokoła tej tworzącej walca, która przechodzi przez

A lokalizacja 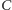pozwala na skonstruowanie trójkąta Wtedy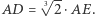

Zapewne wielu zauważy, że to jakby zupełnie coś innego, niż to, co chcemy uznawać za konstrukcję. Wynika z tego pytanie, jak to się stało, że dziś dla nas konstrukcja musi być wykonywana na płaszczyźnie i to wyłącznie cyrklem i linijką. Czyżby znalazł się dyktator, który to zarządził? Z przykrością należy odpowiedzieć: TAK.

Po upowszechnieniu konstrukcji Archytasa z filipiką przeciw niemu (no, może nie z filipiką, bo mowy Demostenesa miały miejsce później) wystąpił Platon.

Stwierdził, że używanie do konstrukcji struktur przestrzennych, a zwłaszcza powstających mechanicznie, urąga matematyce, która na czystej kontemplacji polegać powinna (to wziął dwa tysiąclecia później pod uwagę Nobel i tym uzasadnił nieprzyznanie matematykom nagrody). A czysta kontemplacja powinna operować jedynie tak ulotnym i niepraktycznym obiektem, jak - nieistniejąca przecież realnie - płaszczyzna i manipulować wyłącznie liniami doskonałymi, a więc w każdym punkcie jednakimi, jakimi na płaszczyźnie są jedynie proste i okręgi.

O dziwo, ta argumentacja okazała się przekonywająca i matematycy pokornie przyjęli dyktat Platona. Samo zaś rozważanie przeciwstawienia czystej kontemplacji, jaką powinna być nauka, ponurej praktyczności (jakby Elojów Morlokom) uznane zostało za niezbędny element wykształcenia kulturalnego człowieka i było nauczane aż do I wojny światowej nawet w gimnazjach klasycznych, gdzie matematyka była obecna tylko śladowo.

Dokumentem takich rozważań jest wiersz Cypriana Norwida poświęcony zadumie nad zdegradowaniem kontemplacji.

PLATO I ARCHITA

ARCHITA

Geometrycznej nieświadom nauki Widziałem prosty lud, kładący bruki, I, jako kamień jedna się z kamieniem, Baczyłem, stojąc pod filarów cieniem - Aż żal mi było bezwiedności gminu, Mimo że wieczną on jest wagączynu!... Więc - Geometrii myślane promienie (Rzeknę) gdy z głazem złączę i ożenię, Sferyczność w drzewie wykłuwszy toporem Siłami ramion pchnę brązowe walce, Promienne jeśli kołom natknę palce... To - któż wie...

PLATO

Boskie zmysłowiąc obrysy, Archito! - koturn rzucisz za kulisy - Języka lotność niebieskiego zgrubisz*, Więc Filozofię, Grecję może, zgubisz...

ARCHITA

O! Plato... padam przed prawdy bezkońcem, I nieraz, myśli z drzewa ciosząc, płaczę, Tak wielce wszystko przesiąkłe jest słońcem, Któremu nie ty, ni ja biegów znaczę; Dlatego świętych nie zniżę arkanów, Ani ojczyzny krągłą tarcz wyszczerbię, Owszem: z tych, które rażą cię dziś, planów, Z kres tych na Grecji idealnym herbie, Z liczebnych równań w sił zmienionych dźwignie (Lubo promienność uroku w nich stygnie), Któż wie? - powtarzam - czy lud w sobie drobny, Bezsilny ciałem - jak wyspa osobny, Sykulów mówię, na przykład, siedziba**, Tą siły ramion zmnożywszy nauką, Nie zdoła bronić się jak morska ryba?...

PLATO

Przyjdzie - i tobie dzień zwycięstwa - sztuko!...