Deltoid

Czarno-białe mapy

Słynne twierdzenie orzeka, że każdą mapę da się pomalować najwyżej czterema barwami. Oczywiście, zawsze należy malować tak, by sąsiadujące ze sobą państwa miały różne kolory. Są jednak mapy, dla których wystarczy mniej barw.

Zauważmy, że jeśli mapa ma wierzchołek nieparzystego stopnia, to do pomalowania schodzących się w nim krajów nie wystarczą dwa kolory (Rys. 1).

Twierdzenie. Mapę można pomalować dwoma kolorami wtedy i tylko wtedy, gdy każdy jej wierzchołek jest stopnia parzystego.

Dowód. Implikacja w jedną stronę wynika z powyższej obserwacji.

Dla dowodu drugiej implikacji rozważmy mapę, której każdy wierzchołek ma stopień parzysty. Pomalujmy dowolnie wybrany kraj 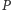$|P$ na czarno. Następnie każdy inny kraj 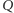$Q$ połączmy z 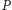$P$ dowolną drogą nieprzechodzącą przez wierzchołki mapy i pomalujmy też na czarno, jeśli droga ta przekracza parzystą liczbę granic, lub na biało, jeśli nieparzystą. Aby zakończyć dowód, należy wykazać, że kolor państwa 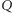$Q$ nie zależy od wyboru drogi.

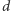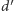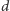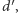Rozważmy dwie różne drogi $d$ i $|d′$ i deformujmy $|d$ do $d ′,$ "mijając" kolejne wierzchołki jak na rysunku 2 Dla wierzchołka stopnia 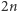$|2n$ droga, zamiast pewnych 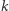$|k$ krawędzi z niego wychodzących, przecina po deformacji pozostałych 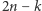$2n − k$ jego krawędzi. Liczby te są tej samej parzystości, zatem taka zmiana nie wpływa na kolor państwa 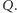$Q.$ Stąd faktycznie kolor ten nie zależy od wyboru drogi.

Rozważmy dowolną spójną mapę (tzn. w jednym kawałku), której każdy wierzchołek ma stopień parzysty i pomalujmy ją dwiema barwami. Następnie przekształćmy tę mapę w jeden duży jednobarwny region w sposób przedstawiony na rysunku 3 (warto zastanowić się, dlaczego zawsze jest to możliwe!). Wówczas obwód tego regionu wyznacza sposób narysowania całej pierwotnej mapy bez odrywania ołówka od kartki i z powróceniem do punktu wyjścia.