Deltoid
Dwa trójkąty
Twierdzenie 1 (*). Dane są trójkąty 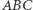 i
i 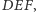 przy czym
przy czym 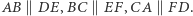 Wówczas istnieje jednokładność lub przesunięcie przeprowadzające
Wówczas istnieje jednokładność lub przesunięcie przeprowadzające 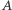 na
na 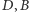 na
na 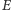 i
i 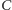 na
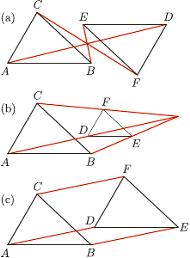
na 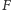 (Rys. 1). Innymi słowy, proste
(Rys. 1). Innymi słowy, proste 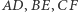 przecinają się w jednym punkcie (środku jednokładności) lub są równoległe.
przecinają się w jednym punkcie (środku jednokładności) lub są równoległe.
Dwa trójkąty spełniające założenia twierdzenia 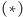 nazwiemy zgodnie ułożonymi, jeśli równoległe wektory
nazwiemy zgodnie ułożonymi, jeśli równoległe wektory 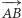 i
i 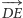 mają ten sam zwrot (Rys. 1 (b) i (c)) oraz niezgodnie ułożonymi w przeciwnym przypadku (Rys. 1 (a)). Dla trójkątów niezgodnie ułożonych przekształcenie opisane w twierdzeniu jest jednokładnością o skali ujemnej, czyli odcinki
mają ten sam zwrot (Rys. 1 (b) i (c)) oraz niezgodnie ułożonymi w przeciwnym przypadku (Rys. 1 (a)). Dla trójkątów niezgodnie ułożonych przekształcenie opisane w twierdzeniu jest jednokładnością o skali ujemnej, czyli odcinki 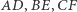 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Więcej o jednokładnościach w Deltoidzie 1/2010, Deltoidzie 2/2010 i Deltoidzie 3/2010, w tym m.in. nieco inne rozwiązanie zadania 4.