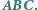O własnościach prostej Simsona
W niniejszym artykule przybliżymy własności jednej z najsłynniejszych prostych w geometrii euklidesowej - prostej Simsona. Jej odkrycie przypisywane jest szkockiemu matematykowi, Robertowi Simsonowi, choć w żadnej jego pracy nie znajdujemy wzmianki o niej.
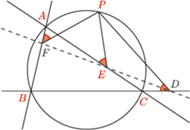
Twierdzenie 1 (Simson). Dany jest trójkąt 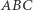 wpisany w okrąg
wpisany w okrąg  oraz punkt
oraz punkt 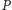 leżący na tym okręgu. Rzuty prostokątne punktu
leżący na tym okręgu. Rzuty prostokątne punktu 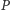 na proste
na proste 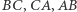 oznaczmy odpowiednio przez
oznaczmy odpowiednio przez 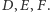 Wówczas punkty
Wówczas punkty 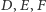 leżą na jednej prostej. Prosta ta nazywana jest prostą Simsona punktu
leżą na jednej prostej. Prosta ta nazywana jest prostą Simsona punktu  względem trójkąta
względem trójkąta  .
.
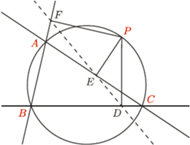
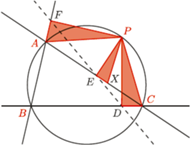
Dowód. Zauważmy, że trójkąty prostokątne 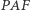 i
i 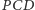 są podobne. Rzeczywiście, wynika to z równości
są podobne. Rzeczywiście, wynika to z równości 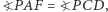 która jest konsekwencją tego, że punkty
która jest konsekwencją tego, że punkty 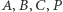 leżą na jednym okręgu. Jest też jasne, że trójkąty te są tak samo zorientowane. Obierzmy na prostej
leżą na jednym okręgu. Jest też jasne, że trójkąty te są tak samo zorientowane. Obierzmy na prostej 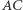 taki punkt
taki punkt 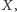 że trójkąt
że trójkąt 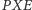 jest podobny do trójkąta
jest podobny do trójkąta 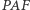 i tak samo zorientowany. Przekształcenie będące złożeniem obrotu o kąt
i tak samo zorientowany. Przekształcenie będące złożeniem obrotu o kąt 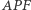 z jednokładnością o skali
z jednokładnością o skali 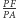 przeprowadza punkty
przeprowadza punkty 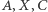 odpowiednio na punkty
odpowiednio na punkty 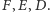 Ponieważ obroty i jednokładności zachowują współliniowość punktów, więc ze współliniowości punktów
Ponieważ obroty i jednokładności zachowują współliniowość punktów, więc ze współliniowości punktów 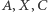 wynika współliniowość punktów
wynika współliniowość punktów 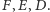
Prawdziwe jest też twierdzenie odwrotne: jeśli punkty 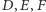 są współliniowe, to punkt
są współliniowe, to punkt 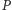 leży na okręgu
leży na okręgu 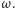 Dowód tego faktu jest dość podobny, nietrudno bowiem sprawdzić, że przy takich założeniach obrót o kąt
Dowód tego faktu jest dość podobny, nietrudno bowiem sprawdzić, że przy takich założeniach obrót o kąt 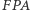 z jednokładnością o skali
z jednokładnością o skali 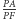 przeprowadzi
przeprowadzi 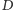 na
na 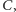 skąd wnioskujemy podobieństwo trójkątów
skąd wnioskujemy podobieństwo trójkątów 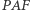 i
i 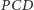 oraz tezę twierdzenia odwrotnego.
oraz tezę twierdzenia odwrotnego.
Jedno z ciekawych uogólnień prostej Simsona polega na rzutowaniu punktu 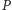 pod dowolnym (ustalonym) kątem. Mówi o tym następujące twierdzenie:
pod dowolnym (ustalonym) kątem. Mówi o tym następujące twierdzenie:
Twierdzenie 2. Dany jest trójkąt 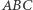 wpisany w okrąg
wpisany w okrąg 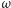 i punkt
i punkt 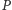 leżący na nim. Niech
leżący na nim. Niech 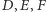 będą takimi punktami odpowiednio na prostych
będą takimi punktami odpowiednio na prostych 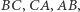 że zachodzą równości kątów skierowanych
że zachodzą równości kątów skierowanych 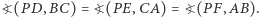 Wówczas punkty
Wówczas punkty 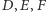 leżą na jednej prostej. Twierdzenie odwrotne również jest prawdziwe.
leżą na jednej prostej. Twierdzenie odwrotne również jest prawdziwe.
Powyższe twierdzenie można udowodnić, wykorzystując analogiczny argument jak w twierdzeniu Simsona. Uzupełnienie szczegółów pozostawiamy Czytelnikowi.
Inne uogólnienie twierdzenia Simsona można otrzymać, badając pola trójkątów o wierzchołkach będących rzutami dowolnego punktu płaszczyzny. Francuz Joseph Gergonne odkrył i jako pierwszy udowodnił poniższy fakt.
Twierdzenie 3. Dane są trójkąt 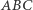 wpisany w okrąg o środku
wpisany w okrąg o środku 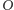 oraz liczba rzeczywista
oraz liczba rzeczywista 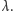 Dla dowolnego punktu
Dla dowolnego punktu 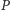 oznaczmy jego rzuty na proste
oznaczmy jego rzuty na proste 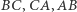 przez
przez 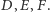 Zbiór punktów
Zbiór punktów 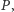 dla których zorientowane pole trójkąta
dla których zorientowane pole trójkąta 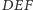 wynosi
wynosi 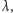 jest albo zbiorem pustym, albo jednoelementowym zbiorem zawierającym punkt
jest albo zbiorem pustym, albo jednoelementowym zbiorem zawierającym punkt  albo pewnym okręgiem o środku
albo pewnym okręgiem o środku 
Dowód powyższego twierdzenia pominiemy, natomiast wywnioskujemy z niego twierdzenie Simsona. Przyjmując 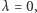 otrzymujemy, że wszystkie punkty, których rzuty na proste
otrzymujemy, że wszystkie punkty, których rzuty na proste 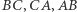 są współliniowe, tworzą pewien okrąg. Nietrudno przekonać się, że rzuty punktów
są współliniowe, tworzą pewien okrąg. Nietrudno przekonać się, że rzuty punktów 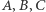 mają tę własność. Wobec tego okręgiem tym musi być okrąg opisany na trójkącie
mają tę własność. Wobec tego okręgiem tym musi być okrąg opisany na trójkącie 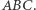
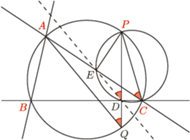
Zanim przejdziemy do próby pokazania ciekawych zastosowań prostej Simsona, udowodnimy kilka interesujących faktów z nią związanych. Zaczniemy od niezwykle użytecznego faktu:
Fakt 1. Dany jest trójkąt 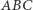 wpisany w okrąg
wpisany w okrąg 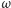 oraz cięciwa
oraz cięciwa 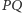 prostopadła do prostej
prostopadła do prostej 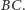 Wówczas prosta Simsona punktu
Wówczas prosta Simsona punktu 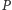 względem trójkąta
względem trójkąta 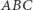 jest równoległa do prostej
jest równoległa do prostej 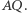
Dowód. Oznaczmy rzuty punktu 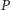 na proste
na proste 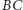 i
i 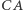 odpowiednio przez
odpowiednio przez 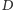 i
i 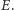 Punkty
Punkty 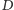 i
i 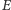 leżą na okręgu o średnicy
leżą na okręgu o średnicy 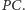 Korzystając z tego, że kąty oparte na tym samym łuku są równe, otrzymujemy
Korzystając z tego, że kąty oparte na tym samym łuku są równe, otrzymujemy 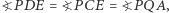 skąd wynika równoległość prostych
skąd wynika równoległość prostych 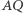 i
i 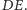
Może się, oczywiście, zdarzyć, że nie istnieje cięciwa przechodząca przez 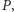 która jest prostopadła do
która jest prostopadła do 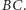 Dzieje się tak dokładnie wtedy, gdy
Dzieje się tak dokładnie wtedy, gdy 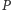 jest jednym z końców średnicy równoległej do
jest jednym z końców średnicy równoległej do 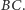 W takim przypadku należy przyjąć
W takim przypadku należy przyjąć 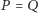 i fakt pozostaje w mocy. Uzupełnienie szczegółów pozostawiamy Czytelnikowi.
i fakt pozostaje w mocy. Uzupełnienie szczegółów pozostawiamy Czytelnikowi.
Na szczególną uwagę zasługuje piękna zależność znaleziona przez szwajcarskiego matematyka Jakoba Steinera, która wiąże prostą Simsona z ortocentrum trójkąta.
Twierdzenie 4 (Steiner). Punkt 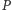 leży na okręgu
leży na okręgu 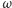 opisanym na trójkącie
opisanym na trójkącie 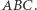 Punkty
Punkty 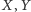 i
i 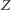 są obrazami punktu
są obrazami punktu 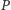 w symetrii względem boków odpowiednio
w symetrii względem boków odpowiednio 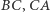 i
i 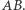 Wówczas punkty
Wówczas punkty 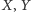 i
i 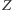 leżą na jednej prostej, która zawiera ortocentrum trójkąta
leżą na jednej prostej, która zawiera ortocentrum trójkąta 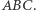 Prostą tę zwykło się nazywać prostą Steinera punktu
Prostą tę zwykło się nazywać prostą Steinera punktu 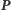 względem trójkąta
względem trójkąta 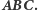
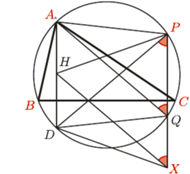
Dowód. Niech  będzie ortocentrum trójkąta
będzie ortocentrum trójkąta  i niech
i niech  będzie takim punktem na
będzie takim punktem na 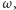 że
że 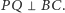 Oznaczmy odbicie
Oznaczmy odbicie 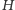 względem
względem 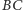 przez
przez 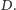 Wówczas
Wówczas

zatem 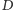 leży na
leży na 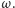 Trapez
Trapez 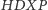 jest równoramienny (jego osią symetrii jest prosta
jest równoramienny (jego osią symetrii jest prosta 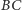 ), wobec tego
), wobec tego 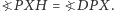 Z drugiej strony trapez
Z drugiej strony trapez 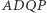 jest wpisany w okrąg, więc również jest równoramienny. Stąd
jest wpisany w okrąg, więc również jest równoramienny. Stąd 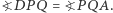 Z powyższych dwóch równości wynika, że
Z powyższych dwóch równości wynika, że 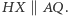 Stąd i z poprzedniego faktu wnioskujemy, że prosta
Stąd i z poprzedniego faktu wnioskujemy, że prosta 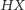 jest równoległa do prostej Simsona punktu
jest równoległa do prostej Simsona punktu 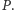 Innymi słowy, punkt
Innymi słowy, punkt 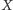 leży na prostej
leży na prostej 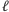 przechodzącej przez
przechodzącej przez 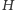 i równoległej do prostej Simsona punktu
i równoległej do prostej Simsona punktu 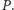 Dokładnie ten sam argument pokazuje, że punkty
Dokładnie ten sam argument pokazuje, że punkty 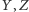 również leżą na
również leżą na 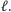
Podobnie jak poprzednio, może się zdarzyć, że punkt 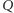 nie będzie istniał. Twierdzenie Steinera pozostaje prawdziwe również w tym przypadku. Uzupełnienie szczegółów ponownie pozostawiamy Czytelnikowi.
nie będzie istniał. Twierdzenie Steinera pozostaje prawdziwe również w tym przypadku. Uzupełnienie szczegółów ponownie pozostawiamy Czytelnikowi.
Twierdzenie Steinera można przeformułować tak: jednokładność o środku w punkcie 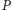 i skali równej 2 przeprowadza prostą Simsona punktu
i skali równej 2 przeprowadza prostą Simsona punktu 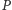 na prostą zawierającą ortocentrum trójkąta
na prostą zawierającą ortocentrum trójkąta 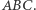 Wypływa stąd wniosek: prosta Simsona punktu
Wypływa stąd wniosek: prosta Simsona punktu 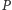 leżącego na okręgu opisanym na trójkącie
leżącego na okręgu opisanym na trójkącie 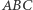 połowi odcinek
połowi odcinek 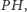 gdzie
gdzie 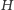 jest ortocentrum trójkąta
jest ortocentrum trójkąta 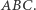 Ponadto środek odcinka
Ponadto środek odcinka 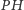 leży na okręgu dziewięciu punktów trójkąta
leży na okręgu dziewięciu punktów trójkąta 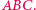 Aby to uzasadnić, wystarczy zauważyć, że skoro odbicia
Aby to uzasadnić, wystarczy zauważyć, że skoro odbicia 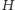 względem boków trójkąta
względem boków trójkąta 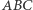 leżą na okręgu opisanym, to okrąg dziewięciu punktów jest jednokładny względem
leżą na okręgu opisanym, to okrąg dziewięciu punktów jest jednokładny względem 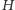 w skali
w skali 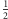 z okręgiem opisanym.
z okręgiem opisanym.
Można również badać relację między dwiema wybranymi prostymi Simsona.
Twierdzenie 5. Punkty 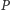 i
i 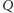 leżą na okręgu
leżą na okręgu 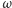 opisanym na trójkącie
opisanym na trójkącie 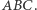 Wówczas miara kąta między prostymi Simsona punktów
Wówczas miara kąta między prostymi Simsona punktów 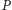 i
i 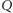 jest równa mierze kąta wpisanego opartego na łuku
jest równa mierze kąta wpisanego opartego na łuku 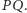
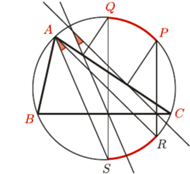
Dowód. Obierzmy punkty 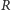 i
i 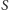 na
na 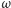 tak, by cięciwy
tak, by cięciwy 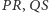 były prostopadłe do prostej
były prostopadłe do prostej 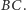 Wówczas proste
Wówczas proste 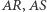 są równoległe do prostych Simsona punktów
są równoległe do prostych Simsona punktów 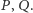 Wobec tego interesujący nas kąt równy jest kątowi między prostymi
Wobec tego interesujący nas kąt równy jest kątowi między prostymi 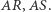 Ten kąt jest oparty na łuku
Ten kąt jest oparty na łuku 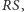 którego długość jest równa długości łuku
którego długość jest równa długości łuku 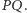
Tutaj również może zdarzyć się, że nie istnieją cięciwy 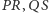 prostopadłe do prostej
prostopadłe do prostej 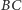 - uzupełnienie dowodu w tym przypadku pozostawiamy Czytelnikowi.
- uzupełnienie dowodu w tym przypadku pozostawiamy Czytelnikowi.
Z powyższych faktów w prosty sposób można wysnuć następujące wnioski:
- Trójkąt
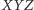 jest wpisany w okrąg opisany na trójkącie
jest wpisany w okrąg opisany na trójkącie 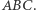 Wówczas proste Simsona punktów
Wówczas proste Simsona punktów 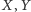 i
i 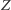 względem trójkąta
względem trójkąta 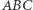 ograniczają trójkąt podobny do trójkąta
ograniczają trójkąt podobny do trójkąta 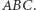
- Proste Simsona dwóch punktów antypodycznych przecinają się pod kątem prostym.
- W trójkącie
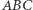 zbiór punktów przecięcia się prostych Simsona dwóch punktów antypodycznych jest jego okręgiem dziewięciu punktów.
zbiór punktów przecięcia się prostych Simsona dwóch punktów antypodycznych jest jego okręgiem dziewięciu punktów.
Nadszedł czas na pokazanie zastosowań prostej Simsona w zadaniach olimpijskich. Część poniższych problemów pochodzi z olimpiad matematycznych o zasięgu międzynarodowym.
Rozważane zadania szybko uległy twierdzeniu Steinera. Tak dzieje się z wieloma problemami dotyczącymi przynależności ortocentrum trójkąta do jakiejś prostej. Dla Czytelników Wnikliwych pozostawiamy kilka zadań, które pomogą zgłębić i odkryć jeszcze więcej własności prostej Simsona.
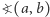 między prostymi
między prostymi 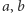 to kąt, o jaki należy obrócić prostą
to kąt, o jaki należy obrócić prostą 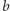 przeciwnie do ruchu wskazówek zegara tak, aby stała się ona równoległa do prostej
przeciwnie do ruchu wskazówek zegara tak, aby stała się ona równoległa do prostej 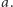
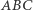 jest: dodatnie, gdy wędrując wzdłuż łamanej
jest: dodatnie, gdy wędrując wzdłuż łamanej 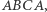 poruszamy się przeciwnie do ruchu wskazówek zegara; ujemne, gdy poruszamy się zgodnie z ruchem wskazówek zegara; zerowe, gdy punkty
poruszamy się przeciwnie do ruchu wskazówek zegara; ujemne, gdy poruszamy się zgodnie z ruchem wskazówek zegara; zerowe, gdy punkty 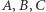 są współliniowe.
są współliniowe.