Okrąg dowpisany
Problem, który opiszę, został zaproponowany przez Amerykanów na LV Międzynarodową Olimpiadę Matematyczną, a jego treść brzmi następująco...
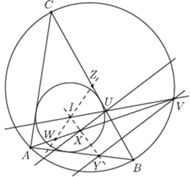
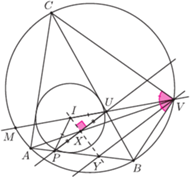
Zadanie. Dany jest trójkąt  Niech
Niech  będzie okręgiem nań opisanym, a
będzie okręgiem nań opisanym, a  środkiem okręgu wpisanego w ten trójkąt. Prosta, przechodząca przez
środkiem okręgu wpisanego w ten trójkąt. Prosta, przechodząca przez 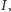 prostopadła do
prostopadła do  przecina odcinek
przecina odcinek 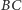 i łuk
i łuk 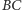 (niezawierający punktu
(niezawierający punktu  ) okręgu
) okręgu 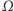 w punktach
w punktach 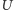 oraz
oraz 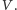 Niech prosta równoległa do
Niech prosta równoległa do 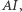 poprowadzona przez
poprowadzona przez 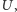 przecina odcinek
przecina odcinek  w punkcie
w punkcie 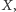 a prosta równoległa do
a prosta równoległa do 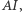 poprowadzona przez
poprowadzona przez 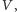 tnie odcinek
tnie odcinek 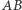 w
w  Oznaczmy kolejno przez
Oznaczmy kolejno przez 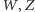 środki odcinków
środki odcinków 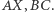 Udowodnić, że jeżeli punkty
Udowodnić, że jeżeli punkty 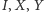 są współliniowe, to również punkty
są współliniowe, to również punkty  są współliniowe.
są współliniowe.
Treść tego zadania wygląda bardzo skomplikowanie. Poczyniono wiele założeń, które na pierwszy rzut oka trudno ze sobą połączyć. Pokażę jednak, że to zadanie można rozwiązać w bardzo elegancki sposób, używając kilku lematów związanych z tzw. mixtilinear incircle. Jest to okrąg, który nie ma fachowej nazwy po polsku, dlatego pozwolę sobie zaproponować dość luźne tłumaczenie tego terminu na okrąg dowpisany. Jego definicja jest następująca: okrąg dowpisany do trójkąta 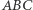 dla wierzchołka
dla wierzchołka 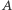 jest to okrąg styczny wewnętrznie do okręgu opisanego na
jest to okrąg styczny wewnętrznie do okręgu opisanego na  oraz styczny do prostych
oraz styczny do prostych 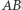 i
i  Zaprezentuję 3 lematy, które przybliżą nam jego własności.
Zaprezentuję 3 lematy, które przybliżą nam jego własności.
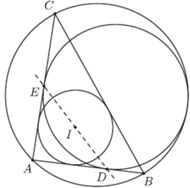
Lemat 1. Dany jest trójkąt  okrąg nań opisany
okrąg nań opisany 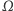 oraz doń dowpisany dla wierzchołka
oraz doń dowpisany dla wierzchołka  Przez
Przez 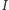 oznaczmy środek okręgu wpisanego w
oznaczmy środek okręgu wpisanego w 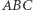 i niech
i niech 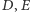 będą punktami styczności okręgu dowpisanego z bokami
będą punktami styczności okręgu dowpisanego z bokami  Wówczas
Wówczas  jest środkiem odcinka
jest środkiem odcinka 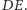
Dowód. Wykażę, że punkty 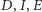 są współliniowe. Wtedy to, że
są współliniowe. Wtedy to, że 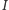 jest środkiem odcinka
jest środkiem odcinka 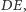 będzie wynikało z tego, że
będzie wynikało z tego, że 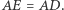 Niech
Niech 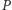 będzie punktem styczności okręgu dowpisanego z
będzie punktem styczności okręgu dowpisanego z 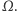 Korzystając z tezy zadania M1468 z Delty 9/15, otrzymujemy, że
Korzystając z tezy zadania M1468 z Delty 9/15, otrzymujemy, że 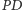 i
i 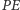 połowią łuki
połowią łuki 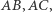 niezawierające kolejno
niezawierające kolejno 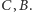 Oznaczmy więc środki tych łuków przez
Oznaczmy więc środki tych łuków przez 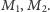 Widzimy teraz, że
Widzimy teraz, że 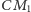 jest dwusieczną
jest dwusieczną 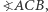 a
a 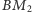 jest dwusieczną
jest dwusieczną 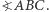 To implikuje współliniowość punktów
To implikuje współliniowość punktów 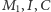 oraz
oraz 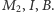 Współliniowość
Współliniowość 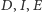 jest teraz konsekwencją twierdzenia Pascala zastosowanego do sześciokąta
jest teraz konsekwencją twierdzenia Pascala zastosowanego do sześciokąta 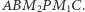
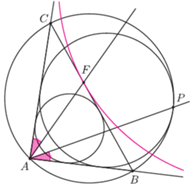
Lemat 2. Przyjmijmy oznaczenia z poprzedniego lematu. Przez  oznaczmy drugi punkt przecięcia
oznaczmy drugi punkt przecięcia 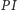 z
z 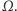 Wtedy
Wtedy 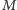 jest środkiem łuku
jest środkiem łuku 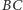 zawierającego
zawierającego 

Dowód. Bez straty ogólności załóżmy, że 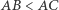 (gdy
(gdy  teza lematu jest trywialna, bo
teza lematu jest trywialna, bo 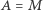 ). Musimy wykazać, że
). Musimy wykazać, że 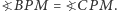 Zauważmy, że
Zauważmy, że

Z racji tego, że 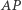 jest zawarty w symedianie
jest zawarty w symedianie 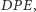 a z poprzedniego lematu wiemy, że
a z poprzedniego lematu wiemy, że  jest środkiem odcinka
jest środkiem odcinka  mamy równość
mamy równość 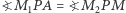 (o symedianach można przeczytać więcej w Delcie 2/2015 i 5/2015). Ponadto
(o symedianach można przeczytać więcej w Delcie 2/2015 i 5/2015). Ponadto

co w połączeniu z poprzednią równością daje tezę.
Lemat 3. Ponownie przyjmijmy oznaczenia jak w poprzednich lematach. Niech 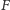 będzie punktem styczności okręgu dopisanego do
będzie punktem styczności okręgu dopisanego do  naprzeciw wierzchołka
naprzeciw wierzchołka  Wynika stąd, że
Wynika stąd, że 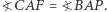
Dowód. Rozważmy inwersję o środku w punkcie  i promieniu
i promieniu 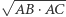 złożoną z symetrią względem dwusiecznej
złożoną z symetrią względem dwusiecznej  Obrazem
Obrazem  w tym przekształceniu jest
w tym przekształceniu jest 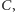 czyli obraz
czyli obraz 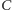 to
to  Zatem
Zatem 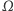 przechodzi na prostą
przechodzi na prostą 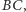 a
a 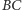 na
na 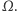 Widzimy więc, że okrąg dowpisany przejdzie na wspomniany okrąg dopisany, skąd wynika, że obrazem
Widzimy więc, że okrąg dowpisany przejdzie na wspomniany okrąg dopisany, skąd wynika, że obrazem  w tym przekształceniu jest
w tym przekształceniu jest 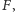 co implikuje, że
co implikuje, że 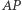 i
i 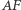 są symetryczne względem dwusiecznej
są symetryczne względem dwusiecznej  To już jest równoważne z tezą lematu.
To już jest równoważne z tezą lematu.

Do rozwiązania zadania przyda się nam jeszcze pewien olimpijski fakt, którego znajomość może okazać się bardzo użyteczna na różnych konkursach matematycznych.
Lemat 4. Niech 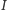 będzie środkiem okręgu wpisanego w trójkąt
będzie środkiem okręgu wpisanego w trójkąt 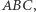 a
a 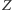 środkiem boku
środkiem boku 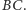 Punkt
Punkt 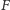 jest punktem styczności okręgu dopisanego do
jest punktem styczności okręgu dopisanego do 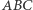 do boku
do boku 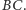 Wówczas odcinki
Wówczas odcinki 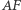 oraz
oraz  są równoległe.
są równoległe.
Dowód. Niech 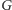 będzie punktem styczności okręgu wpisanego do boku
będzie punktem styczności okręgu wpisanego do boku 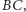 a
a 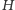 punktem przecięcia prostej
punktem przecięcia prostej 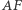 z okręgiem wpisanym (tym, który jest bliżej
z okręgiem wpisanym (tym, który jest bliżej 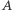 ). Rozważmy jednokładność o środku w
). Rozważmy jednokładność o środku w  która przekształca okrąg dopisany do boku
która przekształca okrąg dopisany do boku 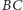 trójkąta
trójkąta 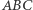 na okrąg wpisany w ten trójkąt. Prosta
na okrąg wpisany w ten trójkąt. Prosta 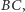 styczna w punkcie
styczna w punkcie 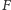 do okręgu dopisanego, przechodzi pod działaniem tej jednokładności na prostą styczną do okręgu wpisanego w punkcie
do okręgu dopisanego, przechodzi pod działaniem tej jednokładności na prostą styczną do okręgu wpisanego w punkcie 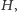 równoległą do
równoległą do 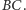 W tej sytuacji
W tej sytuacji 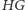 jest średnicą okręgu wpisanego. Pozostaje zauważyć, że
jest średnicą okręgu wpisanego. Pozostaje zauważyć, że 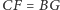 (Czytelnikom, którzy nie spotkali się z tą równością, pozostawiamy ją jako sympatyczne zadanie), w związku z czym
(Czytelnikom, którzy nie spotkali się z tą równością, pozostawiamy ją jako sympatyczne zadanie), w związku z czym 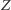 jest środkiem
jest środkiem 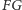 i dlatego z twierdzenia Talesa wynika
i dlatego z twierdzenia Talesa wynika 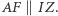
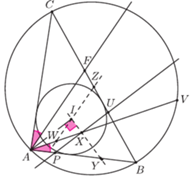
Przystąpmy teraz z powyższym arsenałem do rozwiązania naszego głównego problemu. Przez  będę oznaczał kolejno kąty przy wierzchołkach
będę oznaczał kolejno kąty przy wierzchołkach  Niech prosta
Niech prosta  przecina
przecina  w
w 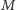 (różnym od
(różnym od  ). Zauważmy, że
). Zauważmy, że 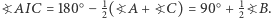 Z kolei
Z kolei  pociąga za sobą
pociąga za sobą 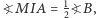 a ponieważ
a ponieważ 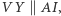 więc
więc 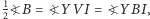 co oznacza, że czworokąt
co oznacza, że czworokąt 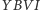 możemy wpisać w okrąg. Niech
możemy wpisać w okrąg. Niech  W podobny sposób pokazujemy, że czworokąt
W podobny sposób pokazujemy, że czworokąt 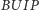 można wpisać w okrąg. Łącząc te spostrzeżenia, otrzymujemy następujące zależności:
można wpisać w okrąg. Łącząc te spostrzeżenia, otrzymujemy następujące zależności:

zatem 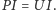 Stosując teraz twierdzenie Talesa do kątów
Stosując teraz twierdzenie Talesa do kątów  i
i 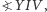 dostajemy:
dostajemy:

skąd wynika, że  czyli
czyli 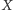 jest środkiem
jest środkiem 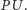 Mamy więc
Mamy więc  Wynika stąd, że
Wynika stąd, że

skąd otrzymujemy, że 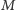 jest środkiem łuku
jest środkiem łuku 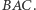 Na mocy lematu
Na mocy lematu 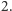 wiemy więc, że
wiemy więc, że 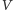 jest punktem styczności okręgu dowpisanego do
jest punktem styczności okręgu dowpisanego do 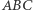 dla wierzchołka
dla wierzchołka 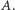 Jeżeli teraz przez
Jeżeli teraz przez  oznaczymy punkt styczności okręgu dopisanego do
oznaczymy punkt styczności okręgu dopisanego do  naprzeciw
naprzeciw 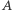 z
z 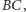 to z lematu
to z lematu 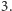 dostaniemy, że
dostaniemy, że 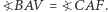 Wynika stąd, że
Wynika stąd, że 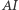 zawiera się w dwusiecznej kąta
zawiera się w dwusiecznej kąta  co w połączeniu z tym, że trójkąt
co w połączeniu z tym, że trójkąt 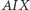 jest prostokątny, pozwala prosto wywnioskować, że
jest prostokątny, pozwala prosto wywnioskować, że  Z drugiej strony, na mocy lematu 4. dostajemy
Z drugiej strony, na mocy lematu 4. dostajemy 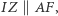 tak więc
tak więc 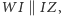 co oczywiście pociąga za sobą tezę zadania.
co oczywiście pociąga za sobą tezę zadania.
Czytelników zatrwożonych stopniem skomplikowania powyższego rozumowania pocieszę tym, że problem został uznany przez jury za najtrudniejszy z geometrycznych. Widać, że znajomość faktów dotyczących okręgu dowpisanego była kluczowym elementem naszego rozwiązania. Czytelnik Uważny może się zastanawiać, czy współliniowość punktów  daje jakieś konkretne zależności, które musi spełniać
daje jakieś konkretne zależności, które musi spełniać 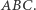 Okazuje się, że istotnie jego boki spełniają zależność
Okazuje się, że istotnie jego boki spełniają zależność 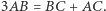 Wykazanie tego faktu pozostawiam Czytelnikom Ambitnym jako olimpijskie ćwiczenie.
Wykazanie tego faktu pozostawiam Czytelnikom Ambitnym jako olimpijskie ćwiczenie.