Mała Delta
Nowości z przeszłości
Punkt, odcinek, trójkąt...
Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.

Sprawa pozornie jasna - dwa punkty, nawet bardzo bliskie, można połączyć odcinkiem punktów pośrednich. Tymczasem... na reprodukowanej w gazecie fotografii można odszukać takie punkty, między którymi nie ma już niczego. Obejrzyjcie taką fotografię pod lupą. Składa się ona ze skończonej ilości czarnych plamek, co widać wyraźnie w powiększeniu. Mimo to odbieramy ją normalnie i na ogół rozpoznajemy, co lub kogo przedstawia.
Płaszczyzna fotografii reprodukowanej w gazecie składa się z izolowanych punktów. Matematycy powiedzieliby o niej, że jest dyskretna. Dyskretny (w matematycznym sensie) jest również obraz na ekranie telewizora, dyskretnym jest także koncert fortepianowy (pod względem wysokości dźwięków, a także ... czasu odmierzanego nutami, półnutami, ćwiartkami, ósemkami itd.)
Na dobrą sprawę żyjemy równolegle w dwóch światach: jeden jest gęsty, spójny, z płynnymi zmianami, a drugi dyskretny. Umiemy jednak jakoś je pogodzić. Zawdzięczamy to właściwościom naszych oczu, uszu i mózgu, że izolowane wrażenia odbieramy jako połączone w sposób ciągły. I całe szczęście, gdyż w przeciwnym wypadku musielibyśmy się obyć bez wielu przyjemności. Na przykład w kinie nie widzielibyśmy płynnego ruchu, tylko ciąg pojawiających się i znikających nieruchomych obrazów.
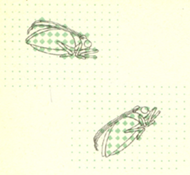
Związki zachodzące między światem "płynnym" a dyskretnym są niekiedy bardzo interesujące. Spójrzmy na rysunek wyobrażając sobie, że jest to oglądany pod lupą ekran telewizora. Trochę upraszczając możemy przyjąć, że linią ciągłą zaznaczone są kontury przedmiotu ujmowanego przez kamerę, natomiast pogrubione kropki to obraz tego przedmiotu oglądany już na ekranie. A więc telewizyjny obraz jest figurą dyskretną. Pola takich dyskretnych figur będziemy mierzyli licząc, z ilu kropek się one składają (jest to chyba sensowna propozycja?).
W tym sensie, pole figury przedstawionej na rysunku jest równe 37. Ale uwaga, oto inny obraz. Kamera ujmuje ten sam przedmiot; tyle tylko, że obrócił się on w stosunku do pierwszego położenia. Jego telewizyjny obraz to jednak coś innego niż poprzednio, gdyż składa się z 31 kropek. Ten pierwszy eksperyment nastawia trochę sceptycznie do możliwości odkrycia sensownych zależności między światem "płynnym" a dyskretnym. Podobne paradoksy są niestety regułą w mikroświecie, to znaczy wtedy, gdy rozmiary rozpatrywanych figur są względnie małe. Co innego jednak, jeśli rozpatrywać będziemy figury duże w stosunku do odstępów między kropkami.
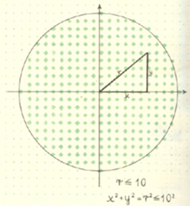
Oto przykład ciekawych zależności. Figura na rysunku to koło o środku w początku układu współrzędnych i o promieniu 10.
Współrzędne punktów jego dyskretnego obrazu, czyli współrzędne grubych kropek, spełniają zależność:

(trzeba przypomnieć sobie twierdzenie Pitagorasa). Grubych kropek będzie tyle, ile jest rozwiązań całkowitych nierówności:

(Pamiętajcie, że rozwiązaniami mogą być nie tylko pary liczb dodatnich, ale i takie pary, w których jedna lub obie liczby są ujemne, na przykład 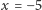 i
i 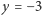 albo
albo 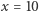 i
i 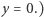 Kto ma cierpliwość może policzyć, że jest ich 317. Z drugiej strony pole rzeczywistego koła filmowanego przez kamerę jest równe
Kto ma cierpliwość może policzyć, że jest ich 317. Z drugiej strony pole rzeczywistego koła filmowanego przez kamerę jest równe 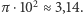
Pole dyskretnego obrazu koła dosyć dobrze przybliża pole rzeczywistego koła... lub na odwrót. Zgodność będzie tym lepsza, im większe będą rozmiary koła. Możemy to wykorzystać w dwie strony. Ci, którzy znają przybliżoną wartość liczby n, mogą obliczyć ile mniej więcej rozwiązań całkowitych ma nierówność:

Ci, którzy umieją dobrze liczyć i mają cierpliwość, mogą spróbować wyznaczyć przybliżoną wartość liczby n (w jaki sposób?).
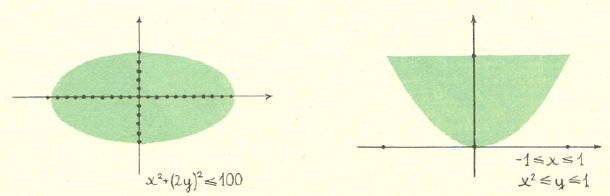
A jak wykorzystać metodę kropek do obliczenia przybliżonych wartości pól figur pokazanych na rysunkach poniżej?