Deltoid
O obrotach
Tym razem o obrotach na płaszczyźnie...
Rys. 1 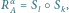 gdzie
gdzie  oznacza złożenie (najpierw stosujemy przekształcenie z prawej strony), a
oznacza złożenie (najpierw stosujemy przekształcenie z prawej strony), a 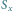 to symetria względem prostej
to symetria względem prostej 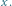
Składanie przekształceń jest łączne: 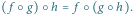
Na płaszczyźnie obrót wokół punktu 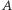 o kąt
o kąt 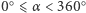 (ozn.
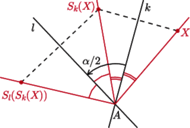
(ozn. 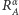 ) jest złożeniem dwóch symetrii osiowych (Rys. 1). Utożsamiamy obroty o
) jest złożeniem dwóch symetrii osiowych (Rys. 1). Utożsamiamy obroty o 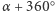 i o
i o 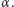
Fakt (*). Dane są kąty 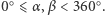 Złożenie
Złożenie 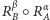 jest:
jest:
a) przesunięciem (być może o wektor zerowy), jeśli 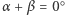 lub
lub 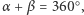
b) obrotem o kąt 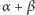 w przeciwnym przypadku.
w przeciwnym przypadku.
Dowód. W każdym przypadku wybieramy osie symetrii 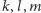 jak przedstawiono na rysunku 2 i uzyskujemy
jak przedstawiono na rysunku 2 i uzyskujemy 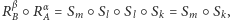 co w zależności od wzajemnego położenia prostych
co w zależności od wzajemnego położenia prostych 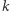 i
i  daje odpowiednie przekształcenia.
daje odpowiednie przekształcenia.
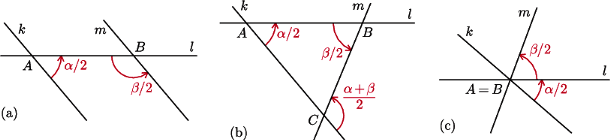
Rys. 2 Jeśli 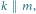 to
to 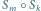 jest przesunięciem, a jeśli
jest przesunięciem, a jeśli 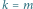 - identycznością (ozn.
- identycznością (ozn. 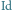 ).
).
Kąty mierzymy antyzegarowo. We wszystkich rozwiązaniach przyjmujemy taką orientację figur, jaką przedstawiono na rysunkach.
Więcej o składaniu symetrii osiowych przeczytać można w Delcie 11/2015
Fakt (**). Kąty 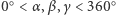 dają w sumie
dają w sumie 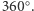 Jeśli różne punkty
Jeśli różne punkty 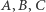 spełniają warunek
spełniają warunek 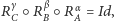 to tworzą trójkąt o kątach odpowiednio
to tworzą trójkąt o kątach odpowiednio 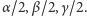
Dowód. Dowód można odczytać z rysunku 2(b).
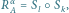 gdzie
gdzie  oznacza złożenie (najpierw stosujemy przekształcenie z prawej strony), a
oznacza złożenie (najpierw stosujemy przekształcenie z prawej strony), a 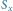 to symetria względem prostej
to symetria względem prostej 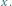
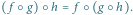
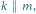 to
to 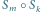 jest przesunięciem, a jeśli
jest przesunięciem, a jeśli 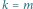 - identycznością (ozn.
- identycznością (ozn. 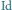 ).
).