Prostokąty na trójkącie
Z twierdzeniem Pitagorasa wszyscy się znamy, budowanie kwadratów na bokach trójkąta prostokątnego nie jest niczym nadzwyczajnym. A co możemy powiedzieć ciekawego o prostokątach skonstruowanych na bokach dowolnego trójkąta?
Okazuje się, że zachodzi następujący fakt:
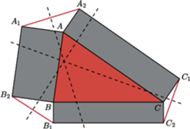
Fakt. Na bokach trójkąta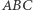 
zbudowano na zewnątrz prostokąty 
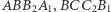i 
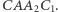Wówczas symetralne odcinków 
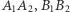i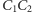 
przecinają się w jednym punkcie.
Czytelnikowi Odważnemu polecamy powalczyć choć chwilę z dowodem powyższego faktu, zaś Czytelnikowi Rozsądnemu radzimy zapoznać się z poniższym lematem (znanym też jako twierdzenie o brytyjskiej fladze) i wtedy spróbować zaatakować nasz fakt, już z większym powodzeniem.
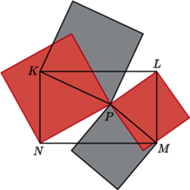
Fakt. Dany jest prostokąt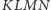 
i dowolny punkt 
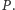Wówczas
Warto odnotować, że jego teza to nic innego jak... budowanie kwadratów na odcinkach! Czytelnik Kreatywny dostrzeże z pewnością małą zbieżność tego faktu z prawdziwą nazwą lematu. Nietrudny dowód pozostawiamy jako ćwiczenie.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (90 KB)