Deltoid
Każdy trójkąt jest równoboczny
Przekształcenie afiniczne płaszczyzny to takie różnowartościowe przekształcenie płaszczyzny w siebie, przy którym obrazem każdej prostej jest prosta. Wszystkie podobieństwa spełniają te warunki, ale nie tylko one...
Niektóre własności przekształceń afinicznych:
- A.
- Zachowują: równoległość prostych, stosunek długości odcinków równoległych, stosunek pól.
- B.
- Są odwracalne i przekształcenia odwrotne do nich również są afiniczne.
- C.
- Każdy trójkąt można przeprowadzić afinicznie na dowolny inny; co więcej, obrazy wierzchołków trójkąta jednoznacznie definiują przekształcenie afiniczne.
Wynika z tego, że dowolny równoległobok można przekształcić afinicznie na dowolny inny (wystarczy przekształcić trzy jego wierzchołki, obraz czwartego zadany jest jednoznacznie przez równoległości podstaw).
- D.
- Każdą elipsę można przekształcić na okrąg, zatem też na dowolną inną elipsę.
Zamiast więc rozważać dany trójkąt, równoległobok czy elipsę, często wystarczy rozważyć odpowiednio trójkąt równoboczny, kwadrat lub okrąg, o ile inne interesujące nas własności są niezmiennikami przekształceń afinicznych (punkt A.).
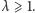 Takie powinowactwo
Takie powinowactwo 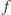 każdy punkt
każdy punkt 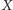 odsuwa
odsuwa 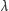 razy dalej od pewnej ustalonej prostej (osi):
razy dalej od pewnej ustalonej prostej (osi):