Deltoid
Jeden obraz mówi więcej niż tysiąc słów
Wiele wzorów na sumy kolejnych liczb naturalnych, ich kwadratów, sześcianów itp. można uzasadnić (lub przynajmniej przekonująco zilustrować) na rysunkach. Często rysunki te wymagają niewiele lub nawet zero komentarza – są to tzw. dowody bez słów...
Rys. 1
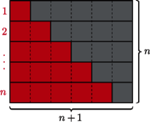
Jednym z najprostszych i najsłynniejszych przykładów jest wzór na sumę kolejnych liczb naturalnych pokazany na rysunku 1:

Korzystając z nieco podobnego pomysłu (Rys. 2) można się przekonać, iż

a więc, na mocy powyższego wzoru na sumę liczb,


Rys. 2

Rys. 3

Rys. 4
Na rysunku 3 można z kolei zobaczyć, że

stąd wzór na sumę trzecich potęg kolejnych liczb naturalnych:

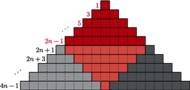
Podobnie można uzyskać wzór na sumę kolejnych liczb nieparzystych (Rys. 4):

Przedstawienie sumy liczb nieparzystych w postaci „piramidy schodkowej” pozwala też udowodnić (Rys. 5) następującą, nieco mniej znaną tożsamość:

Rys. 4
Inny obrazkowy dowód wzoru na sumę liczb nieparzystych przedstawiono w deltoidzie 1/2012, zaś inny dowód wzoru na sumę sześcianów – w deltoidzie 2/2013.