Kosmiczne jaja
Ruch obiegowy Ziemi wokół Słońca przy stałym kierunku osi obrotu planety i nachyleniu do płaszczyzny orbity sprawia, że w ziemskiej pogodzie pojawiają się cyklicznie pory roku. Obecnie promienie słoneczne padają na północną półkulę pod coraz większym kątem, średnia temperatura rośnie, dzień staje się dłuższy, a noc krótsza, co naturalnie skłania do rozważań o odchodzącej zimie i odradzającym się z nadchodzącą wiosną życiu. Zadziwiające, że jednym z wykorzystywanych przez praktycznie wszystkie kultury symbolem wiosny i nowego życia jest jajo...
Występuje ono w odkrywanych przez archeologów obrzędach egipskich, perskich i chińskich, słowiańskich oraz chrześcijańskich. Nie będziemy rozważać tu szczegółów egzegezy symbolu jaja w różnych religiach, zastanowimy się natomiast nad jego kształtem. Okazuje się, że wiele gatunków ptaków znosi jaja niesymetryczne, tj. takie, które z jednej strony są bardziej spłaszczone. Ewolucjoniści tłumaczą tę niesymetryczność naturalną selekcją wynikającą z wpływu środowiska życia danego gatunku: niesymetryczne jajo, które wypadło z gniazda i stacza się po nachylonym zboczu, ma większą tendencję do zatrzymania się w stabilnej pozycji niż jajo symetryczne (jaja żółwi składane w dołach w ziemi są natomiast praktycznie kuliste). Jajo jest także dowodem na doskonałość kształtu kopuły: stosunkowo trudno jest np. zgnieść je w dłoni.
Jak matematycznie opisać kształt jaja? Doskonale wszystkim znany kształt
przekroju podłużnego kurzego jaja nie jest elipsą, ma z nią jednak coś
wspólnego, a związek ten można zaprezentować za pomocą badań
astronomicznych. Jak wiadomo, elipsa to krzywa, po której – według Keplera
i Newtona – poruszają się planety; z definicji suma
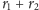 odległości od
ognisk jest w przypadku elipsy stała. Podobną w zamyśle krzywą opisał w 1680
r. francuski astronom Giovanni Cassini, studiując względną odległość Słońca
i Ziemi. W modelu Cassiniego Słońce porusza się wokół Ziemi znajdującej się
w jednym z ognisk po krzywej spełniającej warunek
odległości od
ognisk jest w przypadku elipsy stała. Podobną w zamyśle krzywą opisał w 1680
r. francuski astronom Giovanni Cassini, studiując względną odległość Słońca
i Ziemi. W modelu Cassiniego Słońce porusza się wokół Ziemi znajdującej się
w jednym z ognisk po krzywej spełniającej warunek
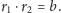 Przy
założeniu, że ogniska znajdują się w odległości
Przy
założeniu, że ogniska znajdują się w odległości
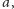 równanie tego
owalu we współrzędnych kartezjańskich to
równanie tego
owalu we współrzędnych kartezjańskich to
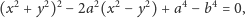 | (1) |
we współrzędnych biegunowych natomiast
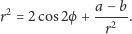 | (2) |
Za charakter krzywej odpowiada wartość parametru
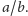 Dla
Dla
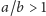 mamy jedną krzywą (dla
mamy jedną krzywą (dla
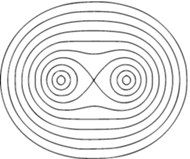
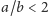 owal jest spłaszczony
i przypomina fistaszek, podczas gdy
owal jest spłaszczony
i przypomina fistaszek, podczas gdy
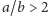 daje krzywą przypominającą
elipsę), natomiast
daje krzywą przypominającą
elipsę), natomiast
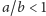 produkuje dwa jajopodobne obrysy.
produkuje dwa jajopodobne obrysy.

Rys. 1 Owale Cassiniego dla różnych wartości parametru
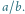
Szczególny przypadek
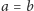 nazywa się lemniskatą Bernoulliego –
otrzymany wtedy kształt wygląda jak symbol nieskończoności i jest
podobny do oglądanej pod odpowiednim kątem wstęgi Möbiusa (lemniscus
to po grecku wstążka). Inną, nietrywialną metodą otrzymania owalu
Cassiniego jest krojenie torusa płaszczyznami równoległymi do jego
osi.
nazywa się lemniskatą Bernoulliego –
otrzymany wtedy kształt wygląda jak symbol nieskończoności i jest
podobny do oglądanej pod odpowiednim kątem wstęgi Möbiusa (lemniscus
to po grecku wstążka). Inną, nietrywialną metodą otrzymania owalu
Cassiniego jest krojenie torusa płaszczyznami równoległymi do jego
osi.
Rys. 2 Owale Cayleya
Pozostając w temacie orbit i oddziaływania grawitacyjnego, podobną
w kształcie do owalu Cassiniego krzywą badał w XIX w. matematyk Arthur
Cayley
 Owale Cayleya to nic innego jak krzywe stałego
potencjału grawitacyjnego (bądź elektrycznego), dla dwóch takich samych
mas (lub ładunków), czyli rozwiązania równania we współrzędnych
dwubiegunowych
Owale Cayleya to nic innego jak krzywe stałego
potencjału grawitacyjnego (bądź elektrycznego), dla dwóch takich samych
mas (lub ładunków), czyli rozwiązania równania we współrzędnych
dwubiegunowych
 | (3) |
Owal Cayleya jest krzywą stopnia ósmego.
Jajo można, oczywiście, otrzymać niewielkim kosztem, zniekształcając nieco elipsę, na przykład w ten sposób:
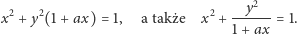 | (4) |
Drugie z powyższych równań daje szczególnie zadowalające kształty dla


Rys. 3 Jajowata krzywa będąca liniowym zniekształceniem elipsy. Obrysy dla parametru
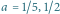 i
i
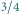 dla drugiego z równań (4)
dla drugiego z równań (4)
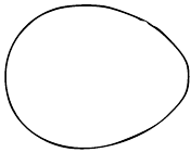
Rys. 4 Jajo Newtona
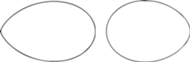
Rys. 5 Listki Keplera (6) i (7), obie krzywe dla parametru
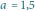
Podobną krzywą opisał w 1710 r. Izaak Newton:
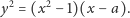 | (5) |
Dla dodatnich wartości parametru
 przypomina ona jajo, w związku
z czym czasami nazywa się ją jajem Newtona (Rys. 4).
przypomina ona jajo, w związku
z czym czasami nazywa się ją jajem Newtona (Rys. 4).
Wśród twórców jajowatych kształtów nie może zabraknąć Johannesa Keplera. Oprócz elips badał on także inne krzywe, na przykład taki oto kształt (zwany czasem listkiem, łac. folium, Keplera),
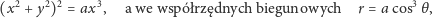 | (6) |
oraz inną krzywą, także zwaną listkiem Keplera,
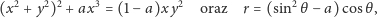 | (7) |
która dla
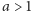 składa się z jednego, obłego kształtu.
składa się z jednego, obłego kształtu.
Jajowatych kształtów opisywanych przez równania analityczne jest, oczywiście, o wiele więcej (http://www.mathematische-basteleien.de/eggcurves.htm), nie wspominając o innych możliwościach otrzymywania podobnych kształtów, np. poprzez konstrukcje geometryczne. Tak powstają np. tzw. jaja Thoma oraz Mossa, przedstawione na rysunku 6. Pierwsza z tych metod, opisana przez szkockiego inżyniera Alexandra Thoma, była być może używana do konstrukcji kamiennych megalitycznych kręgów typu Stonehenge, służących do pomiarów pierwszym badającym niebo archeoastronomom.
Rys. 6 Jajo konstruowalne – metoda Thoma (pierwsze dwa rysunki) i Mossa.
Przybliżając w tym artykule kształt jaja, ograniczyliśmy wybór do wyników otrzymywanych przez historycznych (a nawet prehistorycznych!) astronomów. Wierzymy, że nadchodząca wiosna i związane z nią jajeczne obrzędy będą dobrą motywacją, nie tylko dla Czytelników Dociekliwych, do samodzielnego skonstruowania/narysowania tych nieco mniej standardowych, ale dobrze zasłużonych nauce pisanek.
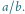
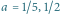 i
i
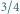 dla drugiego z równań (4)
dla drugiego z równań (4)