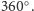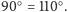Deltoid
Oszustwa
Udowodnimy kilka ewidentnych bzdur, na przykład istnienie okręgu o dwóch
środkach czy równość
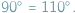 Zachęcam Czytelników
do samodzielnego odszukania błędów w tych dowodach przed lekturą
zamieszczonych na końcu wyjaśnień.
Zachęcam Czytelników
do samodzielnego odszukania błędów w tych dowodach przed lekturą
zamieszczonych na końcu wyjaśnień.
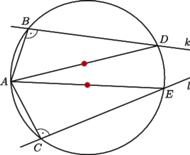
Rys. 1
Dowód. Rozważmy dwie nierównoległe proste
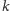 i
i
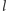 oraz
punkt
oraz
punkt
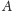 poza nimi (Rys. 1). Punkty
poza nimi (Rys. 1). Punkty
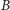 i
i
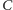 to rzuty punktu
to rzuty punktu
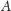 odpowiednio na proste
odpowiednio na proste
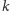 i
i
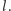 Proste te nie są
równoległe, stąd odcinki
Proste te nie są
równoległe, stąd odcinki
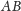 i
i
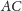 też nie są, więc powstaje
trójkąt
też nie są, więc powstaje
trójkąt
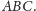
Okrąg opisany na trójkącie
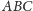 przecina proste
przecina proste
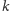 i
i
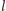 odpowiednio
w punktach
odpowiednio
w punktach
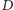 i
i
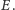 Wtedy
Wtedy
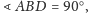 więc odcinek
więc odcinek
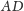 jest średnicą tego okręgu, a środek
jest średnicą tego okręgu, a środek
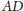 – środkiem
okręgu. Analogicznie
– środkiem
okręgu. Analogicznie
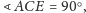 więc odcinek
więc odcinek
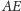 też jest
średnicą okręgu, a środek
też jest
średnicą okręgu, a środek
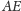 – drugim środkiem okręgu.
– drugim środkiem okręgu.

Rys. 2
Dowód. Rozważmy przecinające się okręgi
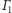 i
i
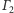 (Rys. 2).
Niech
(Rys. 2).
Niech
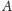 będzie jednym z ich wspólnych punktów oraz niech
będzie jednym z ich wspólnych punktów oraz niech
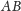 i
i
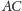 będą średnicami odpowiednio
będą średnicami odpowiednio
 i
i
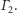 Prosta
Prosta
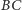 przecina okręgi
przecina okręgi
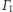 i
i
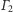 odpowiednio w punktach
odpowiednio w punktach
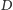 i
i
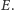
W trójkącie
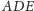 kąt
kąt
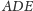 jest prosty jako wpisany w okrąg
jest prosty jako wpisany w okrąg
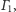 oparty na średnicy
oparty na średnicy
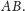 Analogicznie kąt
Analogicznie kąt
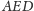 jest
drugim kątem prostym w tym trójkącie.
jest
drugim kątem prostym w tym trójkącie.
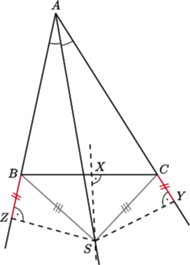
Rys. 3
Dowód. Przypuśćmy, że
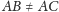 w pewnym trójkącie
w pewnym trójkącie
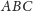 (Rys. 3). Dwusieczna kąta
(Rys. 3). Dwusieczna kąta
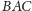 nie jest wtedy wysokością
tego trójkąta, więc przecina symetralną boku
nie jest wtedy wysokością
tego trójkąta, więc przecina symetralną boku
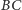 w pewnym punkcie
w pewnym punkcie
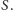 Punkty
Punkty
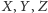 to rzuty punktu
to rzuty punktu
 odpowiednio na proste
odpowiednio na proste
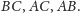
Wówczas
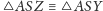 (bo mają równe kąty i wspólny bok
(bo mają równe kąty i wspólny bok
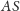 ), stąd
), stąd
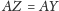 oraz
oraz
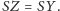 Ponadto
Ponadto
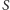 leży
na symetralnej odcinka
leży
na symetralnej odcinka
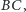 więc
więc
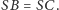
Z ostatnich dwóch równości wynika, że trójkąty prostokątne
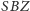 i
i
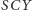 też są przystające, więc
też są przystające, więc
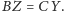 Zatem
Zatem
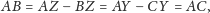 sprzecznie z założeniem.
sprzecznie z założeniem.
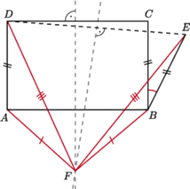
Rys. 4
Dowód. Rozważmy prostokąt
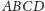 (Rys. 4). Punkt
(Rys. 4). Punkt
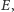 na zewnątrz tego prostokąta, spełnia warunki
na zewnątrz tego prostokąta, spełnia warunki
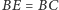 oraz
oraz
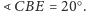 Symetralne odcinków
Symetralne odcinków
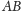 i
i
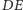 przecinają się
w punkcie
przecinają się
w punkcie
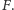 Wówczas
Wówczas
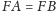 oraz
oraz
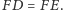 Ponadto
z założenia
Ponadto
z założenia
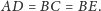 Wobec powyższego trójkąty
Wobec powyższego trójkąty
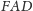 i
i
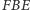 są przystające, a stąd
są przystające, a stąd
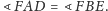
Trójkąt
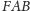 jest równoramienny
jest równoramienny
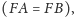 zatem
zatem
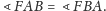
Podsumowując, mamy
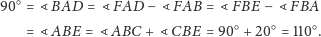
Rozwiązania
Rozwiązanie zadania 1
Rozważany okrąg przechodzi przez punkt przecięcia prostych
 i
i
 Pokrywają się punkty
Pokrywają się punkty
 i
i
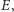 więc również
średnice
więc również
średnice
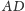 i
i
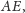 a także ich środki.
a także ich środki.
Rozwiązanie zadania 2
Punkty
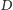 i
i
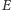 pokrywają się (i znajdują się w punkcie
przecięcia okręgów
pokrywają się (i znajdują się w punkcie
przecięcia okręgów
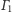 i
i
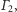 różnym od
różnym od
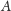 ). Trójkąt
). Trójkąt
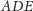 jest więc zdegenerowany do odcinka.
jest więc zdegenerowany do odcinka.
Rozwiązanie zadania 3
Punkt
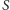 jest środkiem tego łuku
jest środkiem tego łuku
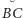 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie
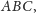 do którego nie należy punkt
do którego nie należy punkt
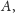 bo środek ten leży i na
dwusiecznej kąta
bo środek ten leży i na
dwusiecznej kąta
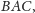 i na symetralnej boku
i na symetralnej boku
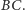 Czworokąt
Czworokąt
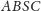 jest więc wpisany w okrąg, stąd
jest więc wpisany w okrąg, stąd
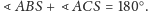 Jeśli
oba te kąty są proste, to
Jeśli
oba te kąty są proste, to
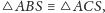 czyli
czyli
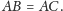 Zatem
jeden z kątów
Zatem
jeden z kątów
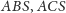 jest ostry, a drugi rozwarty. Przyjmijmy, że
kąt
jest ostry, a drugi rozwarty. Przyjmijmy, że
kąt
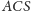 jest ostry. Wówczas punkt
jest ostry. Wówczas punkt
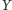 należy do boku
należy do boku
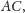 a punkt
a punkt
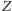 leży poza odcinkiem
leży poza odcinkiem
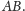 Stąd
Stąd
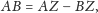 ale
ale
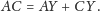
Rozwiązanie zadania 4
Symetralna boku
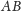 jest jednocześnie symetralną boku
jest jednocześnie symetralną boku
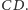 Punkt
Punkt
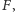 jako punkt przecięcia symetralnych odcinków
jako punkt przecięcia symetralnych odcinków
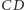 i
i
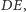 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
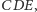 więc leży także na symetralnej odcinka
więc leży także na symetralnej odcinka
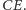 Leży na
niej również punkt
Leży na
niej również punkt
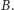 Oznacza to, że trójkąt
Oznacza to, że trójkąt
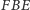 nie
wygląda tak, jak na rysunku 4 – punkt
nie
wygląda tak, jak na rysunku 4 – punkt
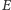 leży po przeciwnej stronie
prostej
leży po przeciwnej stronie
prostej
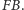 Wobec tego kąt
Wobec tego kąt
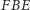 w tym trójkącie nie
jest sumą kątów
w tym trójkącie nie
jest sumą kątów
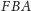 i
i
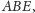 tylko jej dopełnieniem do
tylko jej dopełnieniem do