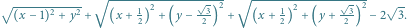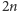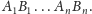Czy matematyk pracuje, czy się bawi?
Zawód matematyka ma wiele zalet...




Homo oeconomicus za główną z nich uważa taniość. Faktycznie, obiekty badań matematyków nie są z tego świata, nie można zatem kupić ich ani w specjalistycznej hurtowni, ani w supermarkecie, ani nawet w osiedlowym sklepiku.
Homo oecologicus jako główną zaletę wymieni fakt, iż matematyczne obiekty nie podlegają cywilizacyjnym zanieczyszczeniom i wynikającym z nich deformacjom.
Homo logisticus wskaże obywanie się bez laboratoriów, a nawet właściwie bez odpowiednich pomieszczeń. Matematykę istotnie można uprawiać wszędzie.
Homo libertinus wskaże niezależność matematyki od ideologii i polityki.
Są wreszcie i tacy, którzy są przekonani, iż myśl matematyczna buja w nieosiągalnych dla niematematyków przestworzach i tym sposobem jest bardziej niezależna niż jakakolwiek inna myśl.
Wszystko to pewnie prawda, ale moje obserwacje kolegów matematyków kazałyby mi wymienić dwie inne, wyróżniające ten zawód zalety. Pierwsza z nich to nieprawdopodobna wręcz obfitość problematyki – nie sposób wymienić sytuację, która nie mogłaby stać się inspiracją do podjęcia matematycznego dociekania. Druga zaś to fakt, że matematyk pracując, bawi się, że praktycznie każda forma zabawy może posłużyć jako alegoria matematycznych dociekań.
Ostatnio miałem okazję zaobserwować to w niemal czystej formie. Jeden z moich kolegów – nazwijmy go Jurkiem – szperał po artykułach w różnych czasopismach, poszukując przykładu zależności, która miała upoglądowić prezentację jego aktualnych prac. I tak trafił na artykuł Junpei Sekino n-Ellipses and the minimum distance sum problem w American Mathematical Monthly, Vol. 106, No. 3 (1999), 193-202.
Niezależnie od powodu napisania wymienionego artykułu, możemy w nim
znaleźć definicję
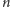 -elipsy jako zbioru punktów, których suma
odległości od danych
-elipsy jako zbioru punktów, których suma
odległości od danych
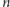 punktów jest stała. Gdy jako punkty
weźmiemy wierzchołki
punktów jest stała. Gdy jako punkty
weźmiemy wierzchołki
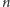 -kąta foremnego, a sumie odległości każemy
być równą odległości jednego z nich od pozostałych, to powstanie właśnie
figura, której własności były potrzebne Jurkowi. W szczególności chciał
wiedzieć, czy krzywa ta jest gładka, czy też może ma dziobki. Oczywiście,
dziobki mogłyby się pojawić tylko w wierzchołkach
-kąta foremnego, a sumie odległości każemy
być równą odległości jednego z nich od pozostałych, to powstanie właśnie
figura, której własności były potrzebne Jurkowi. W szczególności chciał
wiedzieć, czy krzywa ta jest gładka, czy też może ma dziobki. Oczywiście,
dziobki mogłyby się pojawić tylko w wierzchołkach
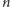 -kąta. Ale jak
stwierdzić, czy są?
-kąta. Ale jak
stwierdzić, czy są?
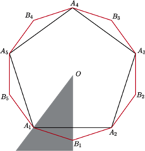
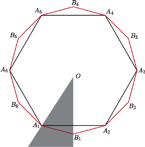
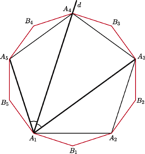
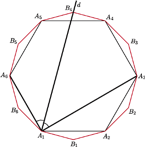
Kiedy zapoznał mnie ze swoim problemem, postanowiłem to sprawdzić w najprostszej sytuacji, czyli dla trójkąta. A że nie miałem sensownego pomysłu, więc zacząłem liczyć, co okazało się do tego stopnia męczące, że tę drogę poszukiwania odpowiedzi uznałem za głupią. Powiedziałem też o tym przy jakiejś okazji koledze – nazwijmy go Zbyszkiem. Ten uznał, że moje trudności to jeszcze jeden przykład na to, jak jestem zacofany, i wpuścił rzecz do Mathematiki, która stwierdziła, że krzywa jest gładka. Ale to mu nie odpowiadało, więc poszukał błędu w swoim wpuszczaniu, znalazł go, poprawił i wtedy Mathematica powiedziała (i pokazała – patrz rysunek), że dziobki są.
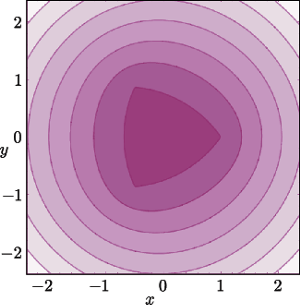
Poziomice funkcji
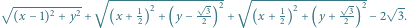
No i wtedy zawstydził się, że zabrał się do geometrii z komputerem – to tak,
jakby z nożem do ryby. Więc rozwiązał problem dla trójkąta metodami
klasycznej geometrii, ale tak go to rozochociło, że odkrył, o co tak naprawdę
w tym problemie chodzi, i rozwiązał go klasycznie dla dowolnego
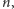 co
jest przedstawione na następnych stronach.
co
jest przedstawione na następnych stronach.
W moim przekonaniu dowodzi to niezbicie tego, od czego zacząłem ten tekst.
Marek
Zadanie (przypadek ogólny). Wykazać, że jeśli
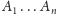 jest
jest
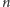 -kątem foremnym, to krzywa płaska
-kątem foremnym, to krzywa płaska
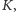 składająca się z punktów
składająca się z punktów
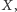 spełniających warunek
spełniających warunek
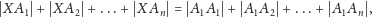 |
ma ostrza w wierzchołkach
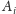 wielokąta.
wielokąta.
Rozwiązanie rozpoczniemy od dowodu następującej obserwacji.
Dowód. Ponieważ symetrie wielokąta
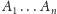 przeprowadzają
krzywą
przeprowadzają
krzywą
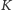 na siebie, wystarczy udowodnić, że każdy punkt
krzywej
na siebie, wystarczy udowodnić, że każdy punkt
krzywej
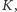 leżący w kącie
leżący w kącie
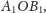 jest punktem trójkąta
jest punktem trójkąta
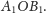
W tym celu rozważmy dwusieczną
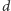 kąta
kąta
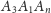 :
:
Gdy
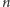 jest nieparzyste, jest to prosta
jest nieparzyste, jest to prosta
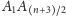 ; gdy
; gdy
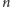 jest
parzyste, dwusieczną jest prosta
jest
parzyste, dwusieczną jest prosta
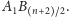
Wykażemy, że
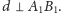 W tym celu zauważmy, że
W tym celu zauważmy, że
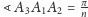 oraz
oraz
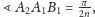 jako kąty wpisane oparte
odpowiednio na
jako kąty wpisane oparte
odpowiednio na
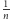 lub
lub
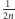 części okręgu opisanego. W podobny
sposób ustalamy, że
części okręgu opisanego. W podobny
sposób ustalamy, że
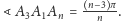 Wobec tego kąt, jaki tworzy
prosta
Wobec tego kąt, jaki tworzy
prosta
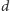 z prostą
z prostą
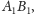 jest równy
jest równy
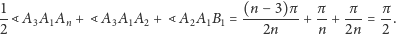 |
Zauważmy, że prosta
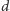 jest też dwusieczną każdego z kątów
jest też dwusieczną każdego z kątów
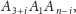 dla
dla
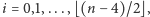 gdyż każdy z tych
kątów powstaje z kąta
gdyż każdy z tych
kątów powstaje z kąta
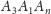 przez odjęcie po obu stronach
dwusiecznej tej samej wielokrotności kąta o mierze
przez odjęcie po obu stronach
dwusiecznej tej samej wielokrotności kąta o mierze
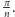
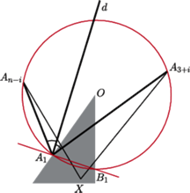
Rozważmy jeden z tych kątów oraz pewien punkt
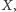 który
należy do kąta
który
należy do kąta
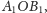 ale leży poza trójkątem
ale leży poza trójkątem
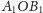 (Rys. 5).
(Rys. 5).
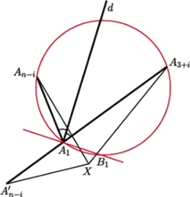
Wykażemy, że
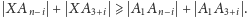 W tym celu
odbijemy punkt
W tym celu
odbijemy punkt
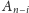 symetrycznie względem prostej
symetrycznie względem prostej
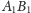 (Rys. 6).
(Rys. 6).
Z tego, że
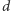 jest dwusieczną kąta
jest dwusieczną kąta
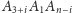 oraz
oraz
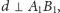 wynika, że punkty
wynika, że punkty
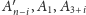 są współliniowe.
Mamy zatem dla
są współliniowe.
Mamy zatem dla
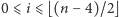

Gdy
 jest liczbą parzystą, każdy z wierzchołków
jest liczbą parzystą, każdy z wierzchołków
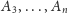 występuje w dokładnie jednej z powyższych nierówności
występuje w dokładnie jednej z powyższych nierówności
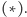 Mamy zatem
Mamy zatem

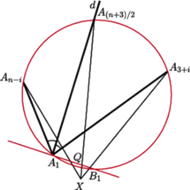
Gdy
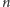 jest liczbą nieparzystą, w nierównościach
jest liczbą nieparzystą, w nierównościach
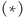 występują
wszystkie wierzchołki
występują
wszystkie wierzchołki
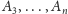 z wyjątkiem
z wyjątkiem
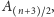 który
wtedy leży na prostej
który
wtedy leży na prostej
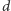 (Rys. 7).
(Rys. 7).
Jeśli
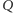 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków
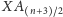 oraz
oraz
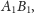 to mamy
to mamy
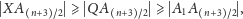 |
gdyż trójkąt
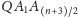 jest prostokątny. Wynika stąd
jest prostokątny. Wynika stąd

W każdym więc przypadku punkt
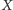 nie należy do krzywej
nie należy do krzywej
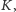 co kończy dowód stwierdzenia.
co kończy dowód stwierdzenia.
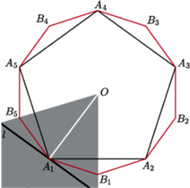
Łatwo teraz wykazać, że krzywa
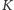 nie jest gładka w punktach
nie jest gładka w punktach
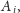 to znaczy nie ma w tych punktach stycznej. Ze względu na
niezmienniczość
to znaczy nie ma w tych punktach stycznej. Ze względu na
niezmienniczość
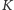 na obroty wielokąta wystarczy przeprowadzić
dowód dla jednego z wierzchołków, np. dla
na obroty wielokąta wystarczy przeprowadzić
dowód dla jednego z wierzchołków, np. dla
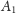 (Rys. 8).
(Rys. 8).
Oczywiście,
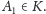 Zauważmy, że punkty krzywej
Zauważmy, że punkty krzywej
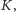 leżące
w pobliżu punktu
leżące
w pobliżu punktu
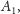 są zawarte w kącie
są zawarte w kącie
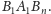 Gdyby
prosta
Gdyby
prosta
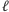 była styczna do krzywej
była styczna do krzywej
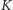 w punkcie
w punkcie
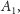 to
z niezmienniczości
to
z niezmienniczości
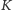 ze względu na symetrię w prostej
ze względu na symetrię w prostej
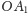 wynikałoby, że
wynikałoby, że
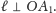 Ale wtedy, z definicji stycznej jako
granicy siecznych wynika, że istnieje taki ciąg punktów
Ale wtedy, z definicji stycznej jako
granicy siecznych wynika, że istnieje taki ciąg punktów
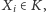 że kąty,
jakie tworzą wektory
że kąty,
jakie tworzą wektory
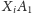 z prostą
z prostą
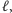 dążą do zera, czyli
dążą do zera, czyli
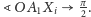 Tymczasem mamy zawsze
Tymczasem mamy zawsze
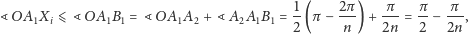 |
sprzeczność, która kończy rozwiązanie zadania.
Udział wzięli Marek KORDOS, Zbigniew MARCINIAK, Jerzy TYSZKIEWICZ