Symetralna i dwusieczna - bliźnięta jedno- czy dwujajowe?
Symetralna to oś symetrii odcinka, a dwusieczna – kąta. W trójkącie tak symetralne, jak dwusieczne, przecinają się w jednym punkcie.
Rozwiążmy zadanie:
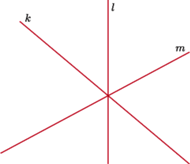
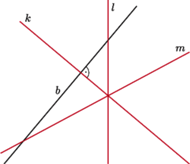
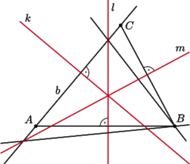
Zadanie 1. Dane są trzy proste przecinające się w jednym punkcie (Rys. 1). Znaleźć trójkąt, dla którego są one
-
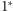
- symetralnymi boków;
-
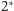
- dwusiecznymi kątów.
Jeśli jakiś trójkąt rozwiązuje nasze zadanie, to każdy jednokładny do
niego względem punktu wspólnego danych prostych też je rozwiązuje.
Możemy więc jeden element trójkąta (w
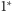 prostą zawierającą
bok, w
prostą zawierającą
bok, w
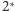 wierzchołek kąta) przyjąć dość dowolnie. Zatem do
roboty!
wierzchołek kąta) przyjąć dość dowolnie. Zatem do
roboty!
Obieramy
-
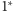
- prostą
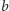 prostopadłą do
prostopadłą do
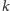 – będzie ona zawierała
wierzchołki
– będzie ona zawierała
wierzchołki
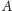 i
i
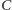 szukanego trójkąta
szukanego trójkąta
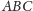 ;
;
-
- punkt
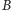 na prostej
na prostej
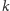 – będzie on wierzchołkiem kąta
– będzie on wierzchołkiem kąta
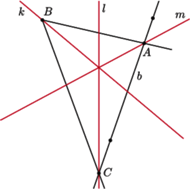
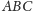 (Rys. 2).
(Rys. 2).
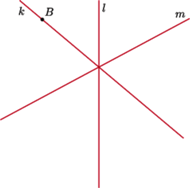
Odbijamy symetrycznie względem
 i
i

-
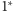
- prostą
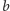 na każdej z otrzymanych prostych musi leżeć
punkt
na każdej z otrzymanych prostych musi leżeć
punkt
 bo jest on obrazem
bo jest on obrazem
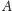 względem
jednej z symetralnych (powiedzmy
względem
jednej z symetralnych (powiedzmy
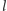 ) i obrazem
) i obrazem
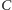 –
względem drugiej;
–
względem drugiej;
-
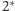
- punkt
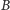 prosta
prosta
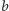 łącząca otrzymane punkty
musi zawierać wierzchołki
łącząca otrzymane punkty
musi zawierać wierzchołki
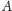 i
i
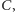 bo obrazy tych
prostych względem dwusiecznych
bo obrazy tych
prostych względem dwusiecznych
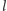 i
i
 przechodzą
przez punkt
przechodzą
przez punkt
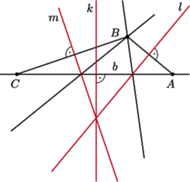
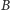 (Rys. 3).
(Rys. 3).
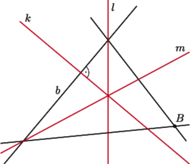
Odbijamy symetrycznie względem
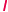 i
i

-

- punkt
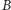 – jego obrazami są punkty
– jego obrazami są punkty
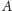 i
i
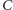 (oczywiście, leżące na prostej
(oczywiście, leżące na prostej
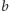 ), co kończy konstrukcję;
), co kończy konstrukcję;
-
- prostą
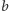 – jej obrazy (oczywiście, przechodzące przez
– jej obrazy (oczywiście, przechodzące przez
 ) wraz z
) wraz z
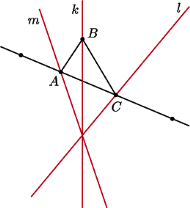
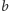 tworzą poszukiwany trójkąt (Rys. 4).
tworzą poszukiwany trójkąt (Rys. 4).
Ostatni krok w konstrukcji
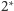 można uprościć, znajdując „na
skróty” i niedualnie punkty
można uprościć, znajdując „na
skróty” i niedualnie punkty
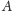 i
i
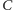 – to przecięcia
– to przecięcia
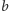 z
z
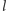 i
i
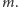
Można więc odnieść wrażenie, że odpowiedź na tytułowe pytanie brzmi: jednojajowe.
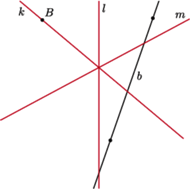
Okazuje się jednak, że wrażenie takie jest mylne, co widać wyraźnie, gdy
weźmiemy inne proste
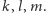
Dla pokazanych obok prostych w wyniku zaproponowanej konstrukcji otrzymujemy, co prawda, jakieś trójkąty (Rys. 5), ale tylko ten, w którym proste mają być symetralnymi, spełnia nasze żądanie, ten drugi jest chyba bez sensu, bo przecięcie dwusiecznych to środek okręgu wpisanego w trójkąt, a ten nie może leżeć na zewnątrz trójkąta.
Powstają dwa pytania:
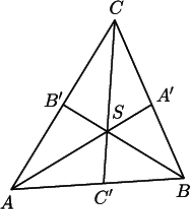
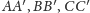 były dwusiecznymi kątów trójkąta
były dwusiecznymi kątów trójkąta
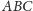 i kąt
i kąt
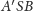 byłby rozwarty, to byłoby
byłby rozwarty, to byłoby
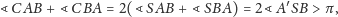
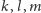 są prostopadłe, a my wybierzemy prostą
są prostopadłe, a my wybierzemy prostą
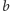 prostopadłą do
trzeciej z nich. Ale wybór jako
prostopadłą do
trzeciej z nich. Ale wybór jako
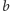 prostej prostopadłej do jednej z prostych
prostopadłych pozwala konstrukcję wykonać.
prostej prostopadłej do jednej z prostych
prostopadłych pozwala konstrukcję wykonać.