Deltoid
W krzywym zwierciadle
Tym razem o inwersji – przekształceniu określanym czasem jako symetria względem okręgu.
Definicja. Obrazem punktu
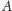 (różnego od
(różnego od
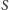 ) w inwersji
względem okręgu
) w inwersji
względem okręgu
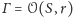 jest taki punkt
jest taki punkt
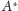 na półprostej
na półprostej
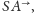 że
że
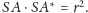
Punkt
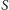 nazywa się środkiem
inwersji. Nie definiujemy jego obrazu
nazywa się środkiem
inwersji. Nie definiujemy jego obrazu
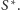
Zauważmy, że:
- obrazem punktu
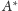 jest punkt
jest punkt
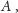
- jeśli punkt
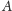 leży na okręgu
leży na okręgu
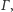 to
to
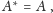
- obraz figury zawartej w pewnym kącie
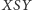 też jest
wewnątrz tego kąta,
też jest
wewnątrz tego kąta,
- obrazem prostej przechodzącej przez punkt
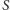 jest ta sama
prosta.
jest ta sama
prosta.
Ogólniej okazuje się, że inwersja zachowuje okręgi i proste. Konkretnie (Rys. 1):
- obrazem okręgu przechodzącego przez punkt
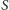 jest prosta
nieprzechodząca przez
jest prosta
nieprzechodząca przez
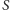 (i na odwrót),
(i na odwrót),
- obrazem okręgu nieprzechodzącego przez
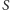 jest okrąg
nieprzechodzący przez
jest okrąg
nieprzechodzący przez
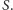
Inwersja to przydatne narzędzie geometryczne. Czasem do rozwiązania zadania wystarczy przekształcić jedynie mały fragment obrazka. Zazwyczaj jednak warto zastosować inwersję do całego rysunku, otrzymując nowy, na ogół kompletnie inny rysunek, na którym często łatwiej dostrzec rozwiązanie. Oto kilka przykładów.

Rys. 1 Niektóre pary figur i ich obrazów w inwersji względem szarego okręgu; na pierwszym i ostatnim rysunku – prosta i okrąg stały.