Wędrówki po okręgu
Matematycy od wielu lat zajmują się wędrówką po okręgu. Jednym z najbardziej
znanych przykładów jest chyba skakanie po nim w określonym kierunku
tak, by między kolejnymi punktami, w których się znajdziemy, była
określona odległość
 (mierzona wzdłuż łuku). Naturalne staje się
wówczas pytanie, czy skacząc tak po okręgu, wrócimy kiedykolwiek do
punktu wyjścia (widać, że rozwiązanie problemu nie zależy od punktu
startowego)? Odpowiedź nasuwa się prędko – powrót nastąpi tylko
wówczas, gdy stosunek długości okręgu do liczby
(mierzona wzdłuż łuku). Naturalne staje się
wówczas pytanie, czy skacząc tak po okręgu, wrócimy kiedykolwiek do
punktu wyjścia (widać, że rozwiązanie problemu nie zależy od punktu
startowego)? Odpowiedź nasuwa się prędko – powrót nastąpi tylko
wówczas, gdy stosunek długości okręgu do liczby
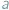 jest liczbą
wymierną. Spróbujmy tym razem powędrować w inny sposób, określony
geometrycznie.
jest liczbą
wymierną. Spróbujmy tym razem powędrować w inny sposób, określony
geometrycznie.

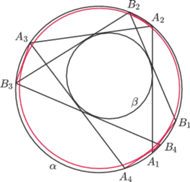
Rys. 1
Oznaczmy nasz okrąg przez
 a w jego wnętrzu umieśćmy drugi
(niekoniecznie współśrodkowy) okrąg
a w jego wnętrzu umieśćmy drugi
(niekoniecznie współśrodkowy) okrąg
 Wędrówka będzie wyglądała
następująco: z punktu
Wędrówka będzie wyglądała
następująco: z punktu
 na okręgu
na okręgu
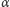 prowadzimy styczną
do okręgu
prowadzimy styczną
do okręgu
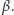 Niech punkt
Niech punkt
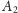 będzie drugim (różnym
od
będzie drugim (różnym
od
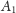 ) punktem przecięcia stycznej z okręgiem
) punktem przecięcia stycznej z okręgiem
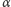 – tam
właśnie powędrujemy. Kolejne kroki wyglądają analogicznie – z punktu
– tam
właśnie powędrujemy. Kolejne kroki wyglądają analogicznie – z punktu
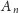 wędrujemy po stycznej do okręgu
wędrujemy po stycznej do okręgu
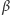 aż do punktu
aż do punktu
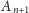 leżącego na okręgu
leżącego na okręgu
 (jak na rysunku 1).
(jak na rysunku 1).
Przy tak określonej wędrówce również pojawia się niejedno pytanie. Czy
wrócimy kiedyś do punktu wyjścia, tak jak na rysunku? I jak wygląda na
 zbiór punktów, do których uda nam się powrócić? Odpowiedzi
okazują się niezwykle zaskakujące – to, czy uda nam się wrócić do punktu
wyjścia, nie zależy od wyboru tego punktu! Jeśli wędrując z pewnego
miejsca, zakończymy wędrówkę, to zaczynając z dowolnego innego miejsca,
również nam się to uda, co więcej – nastąpi to po tej samej liczbie „kroków”,
a w czasie wędrówki tyle samo razy „obejdziemy” okrąg. Mówi o tym
szczególny przypadek tzw. Wielkiego Twierdzenia Ponceleta, który
sformułowany formalnie brzmi następująco:
zbiór punktów, do których uda nam się powrócić? Odpowiedzi
okazują się niezwykle zaskakujące – to, czy uda nam się wrócić do punktu
wyjścia, nie zależy od wyboru tego punktu! Jeśli wędrując z pewnego
miejsca, zakończymy wędrówkę, to zaczynając z dowolnego innego miejsca,
również nam się to uda, co więcej – nastąpi to po tej samej liczbie „kroków”,
a w czasie wędrówki tyle samo razy „obejdziemy” okrąg. Mówi o tym
szczególny przypadek tzw. Wielkiego Twierdzenia Ponceleta, który
sformułowany formalnie brzmi następująco:
Rys. 2
Rys. 13
Twierdzenie. Dany jest okrąg
 oraz okrąg
oraz okrąg
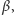 leżący w jego
wnętrzu. Niech
leżący w jego
wnętrzu. Niech
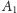 będzie
dowolnym punktem na okręgu
będzie
dowolnym punktem na okręgu
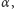 zaś
zaś
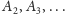 takimi
punktami na
takimi
punktami na
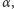 że dla każdego
że dla każdego
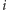 prosta
prosta
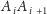 jest
styczna do okręgu
jest
styczna do okręgu
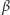 oraz
oraz
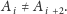 Analogicznie określmy
punkty
Analogicznie określmy
punkty
 Wówczas, jeśli dla pewnego
Wówczas, jeśli dla pewnego
 zachodzi
zachodzi
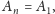 to również
to również
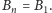
Choć twierdzenie to można udowodnić dzięki metodom geometrii rzutowej,
istnieje również niezwykle pomysłowy dowód wykorzystujący jedynie proste
fakty geometryczne. Rozwiązania wielu problemów geometrii uzyskuje się przez
dorysowanie na rysunku pewnej prostej lub odcinka. Nam przyda się okrąg
(można zobaczyć go na rysunku 2), choć fakt jego istnienia (czyli styczności
wszystkich odcinków
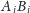 do jednego okręgu) nie jest wcale
oczywisty.
do jednego okręgu) nie jest wcale
oczywisty.
Dowód. Dowód
przeprowadzimy przy założeniu, że
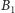 leży po drugiej stronie
prostej
leży po drugiej stronie
prostej
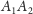 niż okrąg
niż okrąg
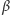 oraz że
oraz że
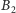 leży po drugiej
stronie prostej
leży po drugiej
stronie prostej
 niż okrąg
niż okrąg
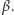 Czytelnik Wnikliwy bez
trudu wykaże, że wynika z tego twierdzenie w całej ogólności. Nie
będziemy również zajmować się przypadkiem, gdy okręgi
Czytelnik Wnikliwy bez
trudu wykaże, że wynika z tego twierdzenie w całej ogólności. Nie
będziemy również zajmować się przypadkiem, gdy okręgi
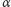 i
i
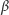 są współśrodkowe – wówczas twierdzenie jest oczywiste.
są współśrodkowe – wówczas twierdzenie jest oczywiste.
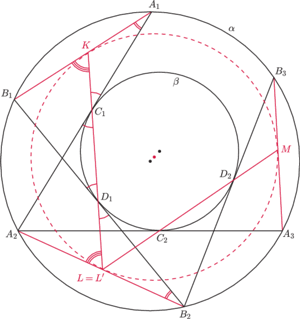
Przyjrzyjmy się punktom
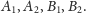 Niech
Niech
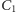 i
i
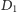 będą odpowiednio punktami styczności
okręgu
będą odpowiednio punktami styczności
okręgu
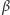 z prostymi
z prostymi
 i
i
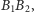 zaś
zaś
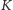 i
i
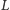 niech będą punktami przecięcia prostej
niech będą punktami przecięcia prostej
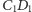 odpowiednio
z odcinkami
odpowiednio
z odcinkami
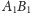 i
i
 (jak na rysunku 3).
(jak na rysunku 3).
Mamy wówczas

oraz
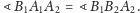 Stąd
Stąd
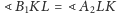 (są to kąty
zewnętrzne w trójkątach
(są to kąty
zewnętrzne w trójkątach
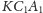 i
i
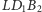 ). W takim razie istnieje
okrąg
). W takim razie istnieje
okrąg
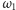 styczny do prostych
styczny do prostych
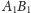 i
i
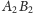 odpowiednio
w punktach
odpowiednio
w punktach
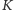 i
i
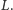 Stosunek pól trójkątów
Stosunek pól trójkątów
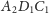 i
i
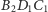 jest równy stosunkowi wysokości opuszczonych na wspólną
podstawę
jest równy stosunkowi wysokości opuszczonych na wspólną
podstawę
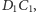 a więc również stosunkowi odcinków
a więc również stosunkowi odcinków
 i
i
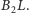 Z tego faktu i z otrzymanych równości kątów wynika,
że
Z tego faktu i z otrzymanych równości kątów wynika,
że

gdzie
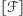 oznacza pole figury
oznacza pole figury
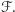 Stąd i z podobieństwa
trójkątów
Stąd i z podobieństwa
trójkątów
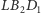 i
i
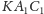 oraz
oraz
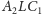 i
i
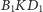 mamy
mamy

Z lematu na marginesie (którego dowód Czytelnik Pracowity może
przeprowadzić z pomocą wskazówek) otrzymujemy wniosek, że środki
okręgów
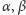 i
i
 są współliniowe.
są współliniowe.
Niech
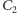 i
i
 będą punktami styczności okręgu
będą punktami styczności okręgu
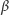 odpowiednio z prostymi
odpowiednio z prostymi
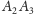 i
i
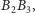 zaś
zaś
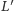 i
i
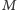 – punktami przecięcia prostej
– punktami przecięcia prostej
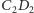 odpowiednio z odcinkami
odpowiednio z odcinkami
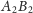 i
i
 Powtarzając wcześniejsze rozumowanie, stwierdzamy,
że istnieje okrąg
Powtarzając wcześniejsze rozumowanie, stwierdzamy,
że istnieje okrąg
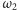 styczny do
styczny do
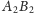 i
i
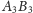 w punktach
w punktach
 i
i
 a jego środek leży na prostej przechodzącej przez
środki okręgów
a jego środek leży na prostej przechodzącej przez
środki okręgów
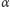 i
i
 Zauważmy, że
Zauważmy, że
 – punkty
te leżą na odcinku
– punkty
te leżą na odcinku
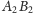 oraz
oraz

Wynika z tego, że okręgi
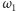 i
i
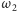 są styczne do prostej
są styczne do prostej
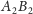 w tym samym punkcie, a ich środki leżą na pewnej ustalonej
prostej
w tym samym punkcie, a ich środki leżą na pewnej ustalonej
prostej
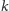 (przechodzącej przez środki okręgów
(przechodzącej przez środki okręgów
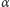 i
i
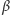 ).
Jeśli
).
Jeśli
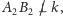 mamy
mamy
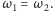 Ten sam wniosek możemy
otrzymać, jeśli
Ten sam wniosek możemy
otrzymać, jeśli
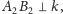 wówczas bowiem punkty
wówczas bowiem punkty
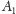 i
i
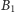 są symetryczne względem prostej
są symetryczne względem prostej
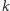 odpowiednio do
punktów
odpowiednio do
punktów
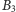 i
i
 więc okręgi
więc okręgi
 i
i
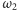 są
symetryczne względem prostej
są
symetryczne względem prostej
 a ich środki leżą na tej prostej.
Czytelnik Spostrzegawczy dostrzeże, że pokazaliśmy w ten sposób
styczność prostej
a ich środki leżą na tej prostej.
Czytelnik Spostrzegawczy dostrzeże, że pokazaliśmy w ten sposób
styczność prostej
 do okręgu
do okręgu
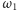 dla dowolnego
dla dowolnego
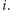
Rys. 4
Przyjrzyjmy się ostatniemu rysunkowi, by dokończyć nasz dowód. Odcinki
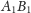 i
i
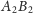 są rozłączne i styczne do okręgu
są rozłączne i styczne do okręgu
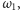 stąd
stąd
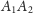 przecina ten okrąg. Skoro
przecina ten okrąg. Skoro
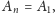 zachodzi również
zachodzi również
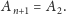 Ponieważ punkty
Ponieważ punkty
 oraz
oraz
 leżą na okręgu
leżą na okręgu
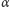 na zmianę (punkt
na zmianę (punkt
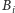 leży po przeciwnej stronie łuku
leży po przeciwnej stronie łuku
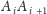 niż okrąg
niż okrąg
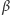 ), to
), to
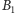 i
i
 leżą na tym
samym łuku
leżą na tym
samym łuku
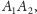 a więc po tej samej stronie prostej
a więc po tej samej stronie prostej
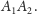 Proste
Proste
 i
i
 są styczne do okręgu
są styczne do okręgu
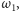 a zatem
a zatem
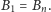
Tak oto znaleźliśmy odpowiedź na pytanie o zbiór punktów, dla których
wędrówka po okręgu
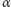 zakończy się po skończonej liczbie kroków –
jest to zbiór pusty lub cały okrąg. Jak jednak rozpoznać, z którą z tych
dwóch sytuacji mamy w danym przypadku do czynienia? Poszukiwanie
odpowiedzi na to i wiele innych pytań pozostawiamy Czytelnikom.
zakończy się po skończonej liczbie kroków –
jest to zbiór pusty lub cały okrąg. Jak jednak rozpoznać, z którą z tych
dwóch sytuacji mamy w danym przypadku do czynienia? Poszukiwanie
odpowiedzi na to i wiele innych pytań pozostawiamy Czytelnikom.
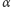 i
i
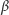 mogą być dowolnymi, niekoniecznie tego
samego rodzaju stożkowymi (elipsami, parabolami, hiperbolami), nie zakłada
się niczego o ich wzajemnym położeniu oraz rozszerza się styczność także
na asymptotyczność.
mogą być dowolnymi, niekoniecznie tego
samego rodzaju stożkowymi (elipsami, parabolami, hiperbolami), nie zakłada
się niczego o ich wzajemnym położeniu oraz rozszerza się styczność także
na asymptotyczność.