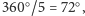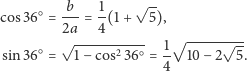Nierówność Ptolemeusza

W klasycznym najczęstszym sformułowaniu twierdzenie Ptolemeusza to:
Twierdzenie 1 (Ptolemeusza). Jeżeli na czworokącie można opisać okrąg, to iloczyn jego przekątnych równa się sumie iloczynów jego przeciwległych boków.
Autorstwo tego twierdzenia jest przypisywane greckiemu matematykowi Ptolemeuszowi pochodzącemu z Tebaidy, który kształcił się i działał w Aleksandrii na początku naszej ery (100-175).
Udowodnimy twierdzenie ogólniejsze zwane nierównością Ptolemeusza:
Twierdzenie 2. Niech
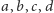 będą kolejnymi bokami dowolnego
czworokąta oraz niech
będą kolejnymi bokami dowolnego
czworokąta oraz niech
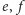 będą jego przekątnymi. Wtedy
będą jego przekątnymi. Wtedy
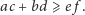 | (*) |
W warunku (*) zachodzi równość wtedy i tylko wtedy, gdy na czworokącie można opisać okrąg.
W dowodzie drugiej części powyższego twierdzenia będziemy korzystali z następującego prostego faktu, często znanego ze szkoły:
Twierdzenie 3. Na czworokącie można opisać okrąg wtedy i tylko wtedy,
gdy sumy jego przeciwległych kątów wynoszą po
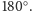
Jego dowód, jak wiadomo, opiera się na dobrze znanym twierdzeniu o kącie środkowym i kątach wpisanych opartych na tym samym łuku.
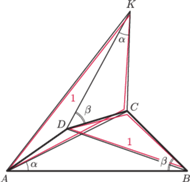
Dowód nierówności Ptolemeusza. Niech
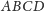 będzie dowolnym czworokątem. Mamy pokazać, że
będzie dowolnym czworokątem. Mamy pokazać, że

Oznaczmy przez
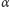 kąt
kąt
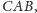 a przez
a przez
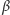 kąt
kąt
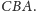 Narysujmy półprostą wychodzącą z punktu
Narysujmy półprostą wychodzącą z punktu
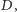 leżącą na
zewnątrz czworokąta
leżącą na
zewnątrz czworokąta
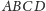 i tworzącą z bokiem
i tworzącą z bokiem
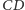 kąt
kąt
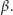 Na tej półprostej wyznaczmy taki punkt
Na tej półprostej wyznaczmy taki punkt
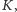 aby kąt
aby kąt
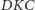 był równy
był równy
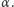 Dzięki temu trójkąty
Dzięki temu trójkąty
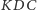 i
i
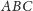 są podobne. Zachodzą zatem proporcje
są podobne. Zachodzą zatem proporcje
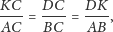 | (1) |
skąd w szczególności wynika, że
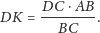 | (2) |
Oznaczmy przez
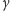 kąt
kąt
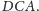 Teraz
Teraz
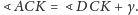 Z trójkąta
Z trójkąta
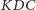 mamy
mamy
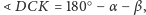 czyli ostatecznie
czyli ostatecznie
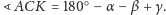 Analogicznie,
Analogicznie,
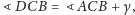 a z trójkąta
a z trójkąta
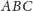 otrzymujemy
otrzymujemy
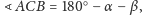 czyli
czyli
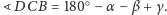 Zatem mamy
Zatem mamy
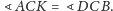 Ponieważ
zachodzi proporcja
Ponieważ
zachodzi proporcja

wynikająca z (1), zatem trójkąty
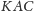 i
i
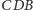 również są
podobne (na rysunku zostały oznaczone kolorem, jedną parę odpowiednich
boków oznaczyliśmy jedynką). Wynika stąd proporcja
również są
podobne (na rysunku zostały oznaczone kolorem, jedną parę odpowiednich
boków oznaczyliśmy jedynką). Wynika stąd proporcja

z której otrzymujemy
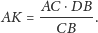 | (3) |
Z nierówności trójkąta wynika, że
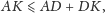 | (4) |
przy czym w warunku tym zachodzi równość wtedy i tylko wtedy, gdy
punkty
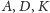 są współliniowe. Podstawiając do tej nierówności
otrzymane wcześniej warunki (2) i (3), otrzymujemy nierówność
są współliniowe. Podstawiając do tej nierówności
otrzymane wcześniej warunki (2) i (3), otrzymujemy nierówność

i mnożąc ją obustronnie przez
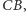 otrzymujemy nierówność
Ptolemeusza.
otrzymujemy nierówność
Ptolemeusza.
Równość w tym warunku jest równoważna faktowi, że w warunku
(4) zachodzi też równość, a to ma miejsce wtedy i tylko wtedy,
gdy punkt
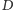 leży na prostej
leży na prostej
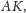 co jest równoważne
równości
co jest równoważne
równości

Równość ta oznacza, że suma kątów wewnętrznych czworokąta, leżących
przy wierzchołkach
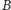 i
i
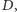 wynosi
wynosi
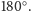 W konsekwencji,
również suma kątów wewnętrznych czworokąta, leżących przy
wierzchołkach
W konsekwencji,
również suma kątów wewnętrznych czworokąta, leżących przy
wierzchołkach
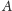 i
i
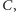 wynosi
wynosi
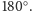 Twierdzenie
pomocnicze gwarantuje, że na czworokącie
Twierdzenie
pomocnicze gwarantuje, że na czworokącie
 można opisać
okrąg.
można opisać
okrąg.
Przykłady prostych zastosowań
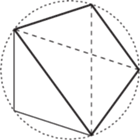
Przykład 1 (Obliczanie przekątnej pięciokąta foremnego).
Rozważmy pięciokąt foremny o boku
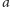 i nazwijmy jego przekątną
i nazwijmy jego przekątną
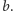 Zbudujemy z jego pomocą czworokąt o trzech bokach będących
bokami pięciokąta i jednym boku będącym przekątną pięciokąta (na rysunku
obok rozważany czworokąt został oznaczony pogrubioną linią).
Zbudujemy z jego pomocą czworokąt o trzech bokach będących
bokami pięciokąta i jednym boku będącym przekątną pięciokąta (na rysunku
obok rozważany czworokąt został oznaczony pogrubioną linią).
Zbudowany czworokąt ma dwie przekątne długości
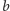 (są to
również
przekątne pięciokąta foremnego) oraz trzy boki równe
(są to
również
przekątne pięciokąta foremnego) oraz trzy boki równe
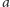 i jeden
bok długości
i jeden
bok długości
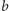 (też przekątna pięciokąta foremnego). Ponieważ
czworokąt jest wpisany w okrąg, zatem zgodnie z twierdzeniem Ptolemeusza
zachodzi równość
(też przekątna pięciokąta foremnego). Ponieważ
czworokąt jest wpisany w okrąg, zatem zgodnie z twierdzeniem Ptolemeusza
zachodzi równość
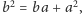 czyli
czyli
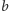 jest tym
rozwiązaniem równania kwadratowego, które wynosi (drugie rozwiązanie
nie interesuje nas, bo jest ujemne)
jest tym
rozwiązaniem równania kwadratowego, które wynosi (drugie rozwiązanie
nie interesuje nas, bo jest ujemne)

Obliczenie przekątnej pięciokąta foremnego bez użycia twierdzenia Ptolemeusza jest bardziej skomplikowane i mozolne.

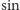 i
i
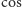 dla kąta
dla kąta
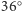 ).
).