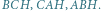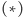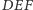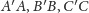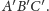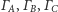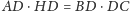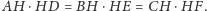Deltoid
Odbicia ortocentrum
Ortocentrum trójkąta to punkt przecięcia jego wysokości. Przyjmijmy
oznaczenia jak na rysunkach 1 i 2 oraz założenie, że trójkąt
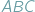 jest
ostrokątny.
jest
ostrokątny.

Rys. 1
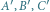 to punkty przecięcia wysokości trójkąta z okręgiem
to punkty przecięcia wysokości trójkąta z okręgiem
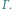
Twierdzenie (*). Punkty
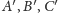 są obrazami ortocentrum
trójkąta
są obrazami ortocentrum
trójkąta
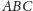 w symetriach względem prostych odpowiednio
w symetriach względem prostych odpowiednio
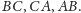
Dowód.
Trójkąty
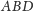 i
i
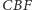 są prostokątne o wspólnym kącie
przy wierzchołku
są prostokątne o wspólnym kącie
przy wierzchołku
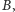 więc
więc
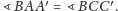 Jednocześnie
Jednocześnie
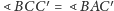 jako kąty wpisane oparte na tym samym łuku.
Stąd
jako kąty wpisane oparte na tym samym łuku.
Stąd
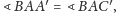 więc trójkąty prostokątne
więc trójkąty prostokątne
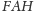 i
i
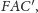 o wspólnym
boku
o wspólnym
boku
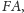 są przystające. Wobec tego
są przystające. Wobec tego
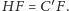 Analogicznie
Analogicznie
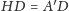 oraz
oraz
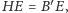 co kończy dowód.
co kończy dowód.
Rys. 2
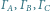 to okręgi opisane odpowiednio na trójkątach
to okręgi opisane odpowiednio na trójkątach
Zadanie 2. Dany jest okrąg
 punkt
punkt
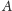 na
nim i punkt
na
nim i punkt
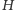 wewnątrz niego. Wpisz w okrąg
wewnątrz niego. Wpisz w okrąg
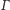 taki trójkąt
o wierzchołku
taki trójkąt
o wierzchołku
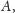 żeby punkt
żeby punkt
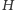 był jego ortocentrum.
był jego ortocentrum.
Zadanie 6. Wykaż, że trójkąt
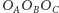 przystaje do trójkąta
przystaje do trójkąta
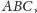 punkt
punkt
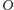 jest jego ortocentrum oraz punkt
jest jego ortocentrum oraz punkt
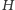 jest
środkiem opisanego na nim okręgu (Rys. 2).
jest
środkiem opisanego na nim okręgu (Rys. 2).
Zadanie 7. Udowodnij, że
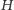 jest jedynym punktem wewnątrz
trójkąta
jest jedynym punktem wewnątrz
trójkąta
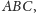 którego obrazy w symetriach względem prostych
którego obrazy w symetriach względem prostych
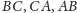 leżą na okręgu
leżą na okręgu
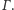
Zadanie 8. Wykaż, że środki okręgów dopisanych do trójkąta i punkty symetryczne do środka okręgu wpisanego w ten trójkąt względem jego wierzchołków leżą na jednym okręgu.
Zadanie 10. Udowodnij, że obrazy symetryczne ortocentrum względem
środków boków trójkąta leżą na okręgu
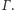 Jak punkty te są
położone względem
Jak punkty te są
położone względem
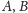 i
i
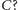
Zadanie 11. Dany jest okrąg
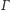 i punkt
i punkt
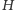 wewnątrz niego.
Wyznacz zbiór środków boków takich trójkątów wpisanych w okrąg
wewnątrz niego.
Wyznacz zbiór środków boków takich trójkątów wpisanych w okrąg
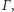 że punkt
że punkt
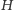 jest ich ortocentrum.
jest ich ortocentrum.
Zadanie 12. Oznaczmy przez
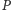 i
i
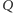 odpowiednio punkty
przecięcia
prostych
odpowiednio punkty
przecięcia
prostych
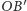 z
z
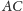 oraz
oraz
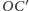 z
z
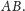 Wykaż,
że istnieje okrąg styczny do prostych
Wykaż,
że istnieje okrąg styczny do prostych
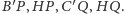
Rozwiązania niektórych zadań
Rozwiązanie (2). Punkt przecięcia prostej
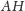 z okręgiem
to
z okręgiem
to
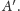 Na mocy
Na mocy
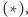 symetralna odcinka
symetralna odcinka
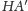 przecina
okrąg
przecina
okrąg
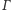 w szukanych punktach
w szukanych punktach
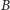 i
i
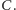
Rozwiązanie (4). Na mocy
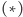 mamy
mamy
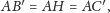 więc
więc
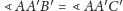 jako kąty
wpisane oparte na równych łukach
jako kąty
wpisane oparte na równych łukach
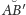 i
i
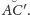 Wobec tego
Wobec tego
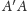 jest dwusieczną kąta
jest dwusieczną kąta
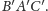 Dowód dla
Dowód dla
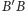 i
i
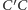 przebiega analogicznie.
przebiega analogicznie.
Rozwiązanie (5). Okręgi
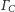 i
i
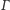 są przystające, jako opisane
na symetrycznych trójkątach
są przystające, jako opisane
na symetrycznych trójkątach
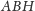 i
i
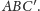 Analogicznie
okręgi
Analogicznie
okręgi
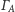 i
i
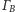 przystają do
przystają do
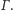
Rozwiązanie (7). Aby obraz punktu
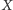 w symetrii względem
w symetrii względem
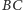 leżał na okręgu
leżał na okręgu
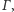 punkt
punkt
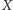 musi leżeć na obrazie okręgu
musi leżeć na obrazie okręgu
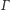 w tej symetrii, czyli na
okręgu
w tej symetrii, czyli na
okręgu
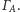 Musi też leżeć na
Musi też leżeć na
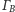 i
i
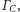 a jedynym
wspólnym punktem tych trzech okręgów jest
a jedynym
wspólnym punktem tych trzech okręgów jest
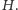
Rys. 3
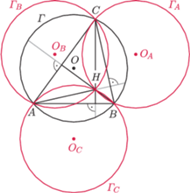
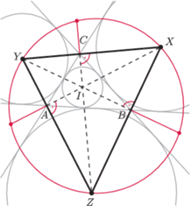
Rozwiązanie (8). Oznaczmy środki okręgów dopisanych przez
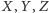 (Rys. 3). Wtedy
(Rys. 3). Wtedy
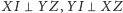 oraz
oraz
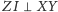 jako dwusieczne kątów przyległych. Stąd
punkt
jako dwusieczne kątów przyległych. Stąd
punkt
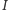 jest ortocentrum trójkąta
jest ortocentrum trójkąta
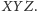 Punkty symetryczne
do
Punkty symetryczne
do
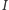 względem wierzchołków wyjściowego trójkąta są odbiciami
ortocentrum
względem wierzchołków wyjściowego trójkąta są odbiciami
ortocentrum
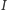 trójkąta
trójkąta
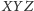 w jego bokach, więc na mocy
w jego bokach, więc na mocy
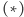 leżą na okręgu opisanym na trójkącie
leżą na okręgu opisanym na trójkącie
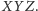
Wskazówka (9). Trójkąty podobne lub potęga punktów
 i
i
 względem okręgu
względem okręgu
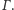
Wskazówka (11). Jest to obraz okręgu
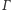 w jednokładności
o środku
w jednokładności
o środku
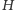 i skali
i skali
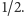
Wskazówka (12). Środkiem szukanego okręgu jest punkt
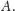
Które z udowodnionych faktów pozostają prawdziwe dla trójkąta
 niekoniecznie ostrokątnego? Które sformułowania wymagają
modyfikacji i jakich?
niekoniecznie ostrokątnego? Które sformułowania wymagają
modyfikacji i jakich?
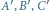 to punkty przecięcia wysokości trójkąta z okręgiem
to punkty przecięcia wysokości trójkąta z okręgiem
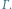
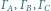 to okręgi opisane odpowiednio na trójkątach
to okręgi opisane odpowiednio na trójkątach