Dowody V postulatu Euklidesa
Oczywiście, V postulatu Euklidesa nie da się dowieść na podstawie poprzednich czterech. Niemniej jednak praktycznie każdy znaczący matematyk od V do XIX wieku taki dowód przeprowadził i dopiero jego koledzy wskazywali, w którym miejscu rozumowania użył przesłanki z czterech początkowych postulatów niewynikającej...
W ten sposób rosła liczba zdań równoważnych V postulatowi, czy – jak kto woli – zdań, które są nieprawdziwe w geometrii nieeuklidesowej powstającej przez zaprzeczenie V postulatu. Niżej przedstawię trzy takie dowody, nie wskazując nieuprawnionych przesłanek. Zostaną one wskazane w następnym numerze Delty.
Najgłupiej postawiony problem matematyki
Oto pięć postulatów, z których Euklides w Elementach wyprowadził całą geometrię i arytmetykę.
- I.
- Od dowolnego punktu do dowolnego innego można poprowadzić prostą.
- II.
- Ograniczoną prostą można dowolnie przedłużyć.
- III.
- Z dowolnego środka dowolnym promieniem można opisać okrąg.
- IV.
- Wszystkie kąty proste są równe.
- V.
- Jeśli suma kątów wewnętrznych jednostronnych, utworzonych przez dwie proste przecięte trzecią, jest mniejsza od dwóch kątów prostych, to proste te po przedłużeniu przetną się i to z tej właśnie strony.
Jak łatwo zauważyć, liczba słów użytych do sformułowania początkowych czterech z nich (27) jest mniejsza od liczby słów potrzebnych do sformułowania piątego (30) – po grecku było podobnie, a przecież postulaty miały wyrażać treści proste i oczywiste.
Zauważył to jeden z epigonów matematyki greckiej, żyjący w czasach słusznie przez niego ocenianych jako lata wszelkiego upadku, Proklos (410–485). Oto jego wnioski i wynikający z nich program.
Nie jest możliwe, aby uczony tej miary co Euklides godził się na obecność tak długiego postulatu w aksjomatyce – obecność postulatu wzięła się z pospiesznego kończenia przez niego Elementów, tak aby zdążyć przed nadejściem słusznie oczekiwanej rychłej śmierci; my zatem – czcząc jego pamięć – powinniśmy ten postulat usunąć lub co najmniej znacznie uprościć.
Choć informację o myślach i stanie zdrowia Euklidesa Proklos wyssał sobie z palca, a ocena treści postulatów poprzez zliczanie słów jest co najmniej cudaczna, to – w co trudno uwierzyć – matematycy uznali program Proklosa za wyzwanie i faktycznie chyba wszyscy próbowali go zrealizować. Spróbujmy i my.
Czym wolno się posługiwać, dowodząc V postulatu?
Dokładniej: jak rozumiano początkowe cztery postulaty (bo są one – jak na dzisiejsze wymagania – sformułowane dość enigmatycznie)? Otóż w tej kwestii panowała całkowita jednomyślność. Można to ująć w trzech punktach.
- Wolno bez ograniczeń wykonywać wszystkie konstrukcje cyrklem i linijką.
oraz przyjmuje się jako dane następujące fakty:
- Na płaszczyźnie prosta, przecinająca jeden z boków trójkąta i nieprzechodząca przez żaden z wierzchołków, przecina jeszcze jeden bok (nazywa się to aksjomatem Pascha).
- Symetrie zachowują wszystkie miary i relacje geometryczne.
Geometria oparta na początkowych czterech postulatach Euklidesa, a właściwie na podanym tutaj rozumieniu ich treści, nazywana jest geometrią absolutną.
Już Proklos zauważył, że
Przez punkt
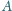 poza prostą
poza prostą
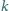 można na płaszczyźnie
poprowadzić prostą
można na płaszczyźnie
poprowadzić prostą
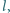 rozłączną z
rozłączną z
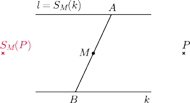
Rys. 1
Istotnie, obierzmy na
 jakiś punkt
jakiś punkt
 i niech środkiem odcinka
i niech środkiem odcinka
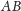 będzie
będzie
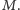 Jako
Jako
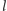 weźmy obraz symetryczny
weźmy obraz symetryczny
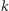 względem
względem
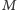 (Rys. 1). Gdyby proste
(Rys. 1). Gdyby proste
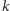 i
i
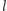 przecinały
się w jakimś punkcie
przecinały
się w jakimś punkcie
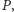 to – ponieważ narysowana figura ma
środek symetrii – również
to – ponieważ narysowana figura ma
środek symetrii – również
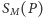 byłby punktem wspólnym
byłby punktem wspólnym
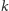 i
i
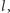 a zatem dwie różne proste przecinałyby się w dwóch
różnych punktach, co jest niemożliwe.
a zatem dwie różne proste przecinałyby się w dwóch
różnych punktach, co jest niemożliwe.
Wynika stąd natychmiast, że V postulat w aksjomatyce geometrii euklidesowej można zastąpić przez
Postulat 1 (Playfaira). Na płaszczyźnie przez każdy punkt poza prostą przechodzi co najwyżej jedna prosta z nią rozłączna.
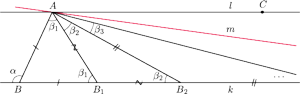
Rys. 2
Nieco trudu trzeba sobie zadać, by wykazać, że podobną rolę pełni
Mianowicie do punktów
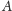 i
i
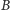 z rysunku 1 dołączmy jeszcze
punkt
z rysunku 1 dołączmy jeszcze
punkt
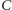 leżący na
leżący na
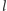 i dowolną prostą
i dowolną prostą
 przechodzącą przez
przechodzącą przez
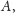 biegnącą poniżej punktu
biegnącą poniżej punktu
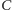 (Rys. 2). Tworzymy na
(Rys. 2). Tworzymy na
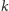 ciąg
punktów, które spełniają warunek
ciąg
punktów, które spełniają warunek
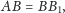
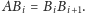 Jak łatwo
zauważyć (oznaczenia z rysunku),
Jak łatwo
zauważyć (oznaczenia z rysunku),
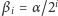 (tu wykorzystujemy
postulat sumy kątów – prawda?). Ponadto
(tu wykorzystujemy
postulat sumy kątów – prawda?). Ponadto
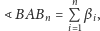 co dla
co dla
 dąży do
dąży do
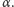
Prosta
 tworzy z odcinkiem
tworzy z odcinkiem
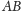 kąt mniejszy od
kąt mniejszy od
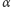 (czemu?),
a więc dla pewnego
(czemu?),
a więc dla pewnego
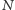 mieści się w trójkącie
mieści się w trójkącie
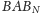 i wobec
tego przecina
i wobec
tego przecina
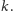
Jeśli więc udowodnimy w geometrii absolutnej postulat Playfaira lub postulat sumy kątów, to udowodnimy tym samym V postulat z początkowych czterech.
Rys. 3
Rys. 4
Rys. 5
Rys. 6
Potrzebne nam w tym celu będą jeszcze cztery twierdzenia geometrii absolutnej
Dokonując symetrii wierzchołka
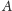 względem środka boku
względem środka boku
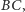 otrzymujemy punkt
otrzymujemy punkt
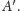 W oznaczeniach z rysunku 3 mamy
W oznaczeniach z rysunku 3 mamy
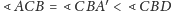 – nierówność zachodzi na mocy
aksjomatu Pascha (trójkąt
– nierówność zachodzi na mocy
aksjomatu Pascha (trójkąt
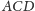 i prosta
i prosta
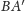 ).
).
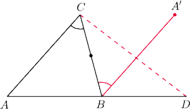
Jeśli
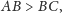 to na odcinku
to na odcinku
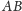 jest taki punkt
jest taki punkt
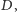 że
że
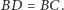 Wówczas (Rys. 4)
Wówczas (Rys. 4)

Ostatnia nierówność wynika z poprzedniego twierdzenia.
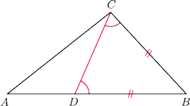
Aby dowieść, że
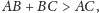 odłóżmy
odłóżmy
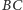 na
przedłużeniu
na
przedłużeniu
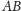 (Rys. 5), otrzymując
(Rys. 5), otrzymując
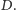 Mamy
Mamy

Stąd na mocy poprzedniego twierdzenia otrzymujemy

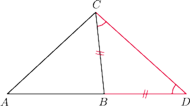
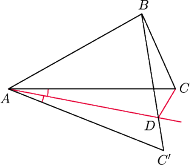
Twierdzenie 4. Jeśli dwa trójkąty mają parę boków odpowiednio równych, to trzeci bok jest dłuższy w tym trójkącie, w którym kąt między nimi jest większy.
Takie dwa trójkąty możemy przemieścić w ten sposób, by jedna
para równych boków pokryła się. Niech więc tymi trójkątami będą
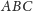 i
i
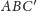 i niech
i niech
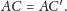 Załóżmy też, że
Załóżmy też, że
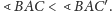 Mamy wykazać, że
Mamy wykazać, że
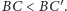 Narysujmy
dwusieczną kąta
Narysujmy
dwusieczną kąta
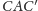 i oznaczmy jej punkt przecięcia z
i oznaczmy jej punkt przecięcia z
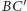 przez
przez
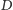 (Rys. 6). Mamy (symetria)
(Rys. 6). Mamy (symetria)
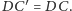 Zatem
Zatem

co wynika z nierówności trójkąta.
Warsztat został skompletowany, przystępujemy do dowodów V postulatu. Każdy z nich przez pewien czas był uznawany za poprawny.
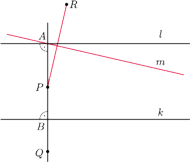
Rys. 7
Dowód postulatu Playfaira – Farkas Bolyai
Oznaczmy przez
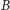 rzut nieleżącego na prostej
rzut nieleżącego na prostej
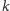 punktu
punktu
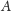 na tę prostą (Rys. 7). Prosta
na tę prostą (Rys. 7). Prosta
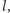 przechodząca przez
przechodząca przez
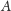 i prostopadła do
i prostopadła do
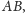 jest rozłączna z
jest rozłączna z
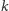 (dlaczego?).
Mamy wykazać, że każda inna prosta
(dlaczego?).
Mamy wykazać, że każda inna prosta
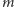 przechodząca przez
przechodząca przez
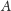 przecina prostą
przecina prostą
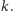 Obierzmy na
Obierzmy na
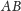 dowolnie punkt
dowolnie punkt
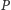 i odbijmy go symetrycznie względem
i odbijmy go symetrycznie względem
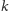 i względem
i względem
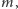 otrzymując, odpowiednio,
otrzymując, odpowiednio,
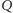 i
i
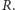 Punkt
Punkt
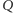 leży
na prostej
leży
na prostej
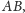 a ponieważ
a ponieważ
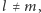 więc
więc
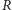 na prostej
na prostej
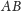 nie leży. Punkty
nie leży. Punkty
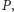
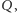
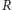 tworzą zatem
trójkąt, a proste
tworzą zatem
trójkąt, a proste
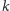 i
i
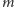 są symetralnymi dwóch jego boków,
a więc obie przechodzą przez środek okręgu opisanego na trójkącie
są symetralnymi dwóch jego boków,
a więc obie przechodzą przez środek okręgu opisanego na trójkącie
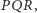 czyli przecinają się.
czyli przecinają się.
Farkas Bolyai (1775–1856), matematyk węgierski, ojciec jednego z odkrywców geometrii nieeuklidesowej.
Dowód postulatu sumy kątów – Adrien-Marie Legendre
Z sumą kątów związane jest pojęcie defektu trójkąta; dla trójkąta
 jest to liczba
jest to liczba

Postulat sumy kątów orzeka, że defekty wszystkich trójkątów są równe 0. Wystarczy więc udowodnić, że defekt nie może być dodatni ani ujemny.
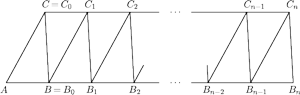
Rys. 8
Przypuśćmy, że defekt trójkąta
 jest ujemny. Ustawmy
wobec tego jego kopie na prostej
jest ujemny. Ustawmy
wobec tego jego kopie na prostej
 tak jak na rysunku 8, oraz
połączmy odcinkami kolejne kopie wierzchołka
tak jak na rysunku 8, oraz
połączmy odcinkami kolejne kopie wierzchołka
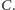 Zauważmy, że
Zauważmy, że
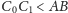 ; wynika to z faktu, iż
; wynika to z faktu, iż
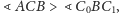 a to dlatego,
że
a to dlatego,
że
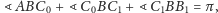 natomiast założyliśmy, że
natomiast założyliśmy, że
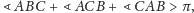 przy czym
przy czym
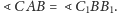
Oznaczmy
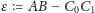 (jest to liczba dodatnia) i obliczmy długość
łamanej
(jest to liczba dodatnia) i obliczmy długość
łamanej
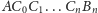 :
:

Nietrudno zauważyć, że dla dużych
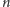 wartość nawiasu będzie
ujemna, a to by znaczyło, że łamana jest krótsza od odcinka – sprzeczność
z nierównością trójkąta.
wartość nawiasu będzie
ujemna, a to by znaczyło, że łamana jest krótsza od odcinka – sprzeczność
z nierównością trójkąta.
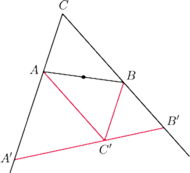
Rys. 9
Zatem trójkątów z ujemnym defektem nie ma. Przypuśćmy, że jest
choćby jeden,
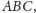 który ma dodatni defekt
który ma dodatni defekt
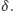 Odbijmy
go symetrycznie względem środka odcinka
Odbijmy
go symetrycznie względem środka odcinka
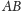 i przez obraz
i przez obraz
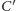 punktu
punktu
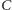 poprowadźmy prostą przecinającą przedłużenia
boków
poprowadźmy prostą przecinającą przedłużenia
boków
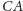 i
i
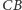 w punktach
w punktach
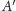 i
i
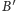 (Rys. 9).
Zauważmy, że defekt trójkąta
(Rys. 9).
Zauważmy, że defekt trójkąta
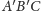 jest sumą defektów czterech
trójkątów, z jakich się składa – suma ta to
jest sumą defektów czterech
trójkątów, z jakich się składa – suma ta to
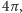 od czego trzeba odjąć
sumy kątów wszystkich trójkątów. Ale w punktach
od czego trzeba odjąć
sumy kątów wszystkich trójkątów. Ale w punktach
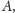
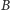 i
i
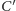 kąty te składają się na
kąty te składają się na
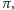 pozostaje więc tylko jedno
pozostaje więc tylko jedno
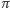 minus suma kątów trójkąta
minus suma kątów trójkąta
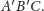 Na mocy pierwszej części
dowodu widzimy, że
Na mocy pierwszej części
dowodu widzimy, że

bo przy symetrii defekt się nie zmienia. Zatem taka operacja zwiększa defekt
trójkąta co najmniej dwukrotnie. Można więc za jej pomocą uzyskać defekt
większy niż
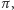 co by znaczyło, że trójkąt ma ujemną sumę kątów –
sprzeczność.
co by znaczyło, że trójkąt ma ujemną sumę kątów –
sprzeczność.
Adrien-Marie Legendre (1752–1833), matematyk francuski, był także autorem podręczników szkolnych; przytoczony dowód władze oświatowe Francji poleciły umieścić w jednym z tych podręczników – jego znajomość obowiązywała uczniów przez ponad 20 lat.
Dowód nie wprost – Girolamo Saccheri
Tym razem rozumowanie jest następujące – przypuśćmy, że postulat sumy
kątów jest nieprawdziwy. Wtedy – posługując się sytuacją z rysunku 2,
uzyskamy rezultat, iż
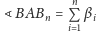 dla
dla
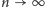 dąży do kąta
dąży do kąta
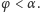 Wówczas prosta
Wówczas prosta
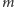 nakreślona tak, by tworzyła z
nakreślona tak, by tworzyła z
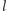 kąt
kąt
 będzie asymptotą prostej
będzie asymptotą prostej
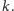 A przecież proste
nie mogą być asymptotyczne.
A przecież proste
nie mogą być asymptotyczne.
Girolamo Saccheri (1667–1733), matematyk włoski – jego prace zapoczątkowały podejrzenia, iż, być może, istnieją inne geometrie niż euklidesowa.
Tyle dowodów – w następnym numerze ci, którzy nie dostrzegli w nich nieuprawnionych przesłanek, będą mogli je znaleźć.
Tym, którzy chcieliby poznać intelektualne i psychiczne męki matematyków przez ponad tysiąc lat bezskutecznie dowodzących V postulatu, polecam wątek Velasqueza w szkatułkowej powieści Jana Potockiego Rękopis znaleziony w Saragossie.