Deltoid
Twierdzenie Brianchona
Poprzedni deltoid poświęcony był osiom potęgowym, między innymi twierdzeniu, które w skrócie brzmi tak: osie potęgowe trzech okręgów przecinają się w jednym punkcie. Ciekawym jego zastosowaniem jest dowód twierdzenia Brianchona.
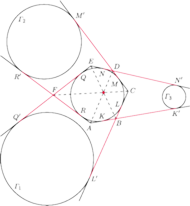
Twierdzenie (Brianchona). Sześciokąt
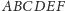 jest opisany na
okręgu. Wówczas przekątne
jest opisany na
okręgu. Wówczas przekątne
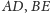 i
i
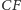 przecinają się
w jednym punkcie.
przecinają się
w jednym punkcie.
Dowód. Oznaczmy okrąg przez
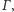 a jego punkty styczności
do boków sześciokąta jak na rysunku 1. Ustalmy pewną długość
a jego punkty styczności
do boków sześciokąta jak na rysunku 1. Ustalmy pewną długość
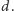 Niech punkt
Niech punkt
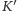 leży na półprostej
leży na półprostej
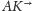 tak, by
tak, by
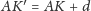 ; stąd
; stąd
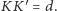 Analogicznie
zdefiniujmy punkty
Analogicznie
zdefiniujmy punkty
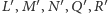 odpowiednio na półprostych
odpowiednio na półprostych
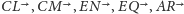 (można
wybrać
(można
wybrać
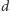 tak, by
tak, by
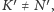
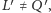
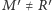 ).
Istnieje okrąg
).
Istnieje okrąg
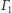 styczny do prostych
styczny do prostych
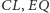 odpowiednio
w punktach
odpowiednio
w punktach
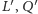 – jest on obrazem
– jest on obrazem
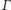 w jednokładności
względem punktu przecięcia prostych
w jednokładności
względem punktu przecięcia prostych
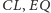 lub przesunięciem
lub przesunięciem
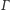 o
o
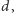 jeśli proste te są równoległe. Analogicznie istnieje
okrąg
jeśli proste te są równoległe. Analogicznie istnieje
okrąg
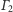 styczny do prostych
styczny do prostych
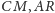 w punktach
w punktach
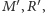 oraz
oraz
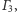 styczny do
styczny do
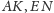 w
w
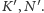 Ponieważ
Ponieważ
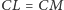 oraz
oraz
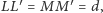 więc
więc

Podobnie ponieważ
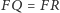 oraz
oraz
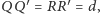 otrzymujemy
otrzymujemy

Prosta
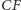 jest
więc osią potęgową okręgów
jest
więc osią potęgową okręgów
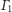 i
i
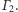 Analogicznie prosta
Analogicznie prosta
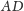 jest osią potęgową
jest osią potęgową
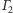 i
i
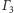 oraz
oraz
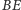 jest osią
potęgową
jest osią
potęgową
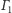 i
i
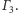 Wobec tego proste
Wobec tego proste
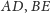 i
i
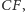 jako osie potęgowe trzech okręgów, przecinają
się w jednym punkcie.
jako osie potęgowe trzech okręgów, przecinają
się w jednym punkcie.
Uwaga. Twierdzenie Brianchona jest też prawdziwe dla sześciokątów zdegenerowanych, a także – ogólniej – dla sześciokątów opisanych na elipsach.