Deltoid
Osie potęgowe
Nieco więcej o potędze punktu względem okręgu.
Pojęcie potęgi punktu z poprzedniego deltoidu (przypomniane na marginesie) prowadzi do poniższych trudniejszych twierdzeń o ciekawych zastosowaniach.
Twierdzenie 1.
Dla niewspółśrodkowych okręgów
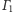 i
i
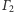 zbiór punktów
zbiór punktów
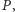 takich że
takich że
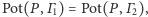 jest prostą, zwaną osią
potęgową okręgów
jest prostą, zwaną osią
potęgową okręgów
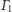 i
i
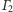 (Rys. 1).
(Rys. 1).

Rys. 1 Przykłady osi potęgowych. Oś potęgowa jest prostopadła do prostej łączącej środki.
Twierdzenie 2. Jeśli środki okręgów
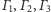 są parami różne,
to osie potęgowe
par okręgów
są parami różne,
to osie potęgowe
par okręgów
 i
i
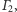
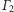 i
i
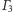 oraz
oraz
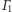 i
i
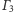 są równoległe (gdy środki tych okręgów są współliniowe) lub
przecinają się w jednym punkcie (w przeciwnym przypadku).
są równoległe (gdy środki tych okręgów są współliniowe) lub
przecinają się w jednym punkcie (w przeciwnym przypadku).
Dowód. Jeśli środki okręgów leżą na jednej prostej, to osie
potęgowe są prostopadłe do niej. W przeciwnym przypadku żadne dwie
osie nie są równoległe; niech
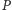 będzie punktem przecięcia osi
będzie punktem przecięcia osi
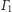 i
i
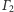 z osią
z osią
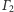 i
i
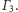 Wtedy
Wtedy

więc
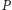 leży też na osi potęgowej okręgów
leży też na osi potęgowej okręgów
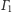 i
i