Osobliwość trójkątów
Zasada Cavalieriego dla figur płaskich brzmi:
jeżeli dwie figury płaskie w
przecięciu z każdą prostą równoległą do danej dają przekrój o tej samej
długości, to pola tych figur są równe.
Pole figury
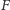 zawartej między prostymi
zawartej między prostymi
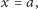
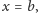 gdzie
gdzie
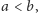 oraz krzywymi
oraz krzywymi
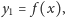
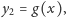 gdzie
gdzie
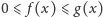 dla
dla
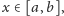 można wyrazić wzorem
można wyrazić wzorem

Jeśli wprowadzimy funkcję
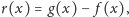 to
to
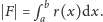 Ostatnia zależność dowodzi, że kształt figury
Ostatnia zależność dowodzi, że kształt figury
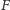 nie ma żadnego znaczenia, ważna jest jedynie długość odcinków
nie ma żadnego znaczenia, ważna jest jedynie długość odcinków
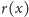 dla różnych wartości zmiennej
dla różnych wartości zmiennej
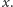 Tę obserwację
wyraża
Tę obserwację
wyraża
Twierdzenie (Zasada Cavalieriego dla figur płaskich). Jeżeli dwie figury płaskie w przecięciu z każdą prostą równoległą do danej dają przekrój o tej samej długości, to pola tych figur są równe.
Przekroje nie muszą nawet być w jednym kawałku – wystarczy, żebyśmy umieli obliczyć sumaryczną długość takiego przekroju. Twierdzenie odwrotne nie jest prawdziwe – istnieją figury o równych polach, których nie można ułożyć na płaszczyźnie tak, że przecinane prostymi równoległymi o wskazanym kierunku, w każdym przypadku będą dawać przekroje o równych długościach.
Twierdzenie 1. Nie istnieje trójkąt
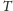 o polu
o polu
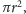 taki że
przekroje pewnego koła o promieniu
taki że
przekroje pewnego koła o promieniu
 i trójkąta
i trójkąta
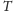 każdą
prostą równoległą do danej są odcinkami o równych długościach.
każdą
prostą równoległą do danej są odcinkami o równych długościach.
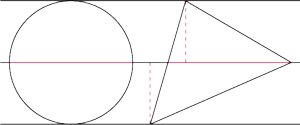
Dowód. Gdyby istniało takie położenie koła o promieniu
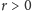 i trójkąta
i trójkąta
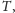 w którym każda prosta o ustalonym
kierunku przecinałaby te figury na odcinkach równej długości (jeśli
w ogóle by je przecinała), to prosta, która przechodziłaby przez środek
koła, musiałaby przechodzić przez jeden z wierzchołków trójkąta i jej
przecięcie z trójkątem miałoby długość
w którym każda prosta o ustalonym
kierunku przecinałaby te figury na odcinkach równej długości (jeśli
w ogóle by je przecinała), to prosta, która przechodziłaby przez środek
koła, musiałaby przechodzić przez jeden z wierzchołków trójkąta i jej
przecięcie z trójkątem miałoby długość
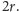 Trójkąt
Trójkąt
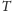 zostałby podzielony na dwa trójkąty, dla których to przecięcie
byłoby wspólną podstawą. Ponieważ opuszczone na nią wysokości
w sumie miałyby długość
zostałby podzielony na dwa trójkąty, dla których to przecięcie
byłoby wspólną podstawą. Ponieważ opuszczone na nią wysokości
w sumie miałyby długość
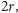 więc pole trójkąta musiałoby być
równe
więc pole trójkąta musiałoby być
równe
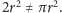 Uzyskana sprzeczność kończy dowód.
Uzyskana sprzeczność kończy dowód.
W przypadku trójkątów o równych polach sytuacja jest całkowicie odmienna, chociaż niełatwo to sobie wyobrazić, gdy patrzymy na dwa trójkąty o równych polach, z których jeden jest „cienki i długi”, a drugi „krótki i pękaty”.
Twierdzenie 2 (H. Eves, 1991). Dla trójkątów o równych polach istnieje takie ich położenie na płaszczyźnie, że każda prosta równoległa do danej przecina każdy z trójkątów na odcinku o tej samej długości.
Dowód. Załóżmy, że trójkąty
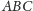 i
i
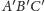 mają
równe pola. Rozpatrzmy dwa przypadki.
mają
równe pola. Rozpatrzmy dwa przypadki.
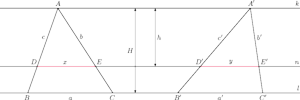
Przypadek 1. Jeden bok trójkąta
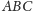 ma taką samą długość
jak jeden bok trójkąta
ma taką samą długość
jak jeden bok trójkąta
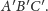 Możemy przyjąć bez straty
ogólności, że
Możemy przyjąć bez straty
ogólności, że
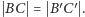 Umieszczamy trójkąty
Umieszczamy trójkąty
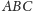 i
i
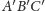 tak, aby boki
tak, aby boki
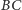 oraz
oraz
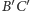 leżały na prostej
leżały na prostej
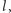 zaś
wierzchołki
zaś
wierzchołki
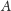 i
i
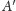 leżały w tej samej półpłaszczyźnie.
Ponieważ trójkąty
leżały w tej samej półpłaszczyźnie.
Ponieważ trójkąty
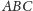 i
i
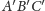 mają równe pola, więc
wierzchołki
mają równe pola, więc
wierzchołki
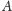 i
i
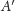 leżą na prostej
leżą na prostej
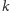 równoległej
do
równoległej
do
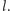 Sprawdźmy, że dla dowolnej prostej
Sprawdźmy, że dla dowolnej prostej
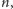 równoległej
do
równoległej
do
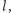 jej przekroje z trójkątami
jej przekroje z trójkątami
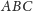 i
i
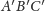 są
równe, czyli
są
równe, czyli
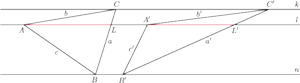
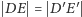 przy oznaczeniach z rysunku. Istotnie,
z twierdzenia Talesa mamy
przy oznaczeniach z rysunku. Istotnie,
z twierdzenia Talesa mamy

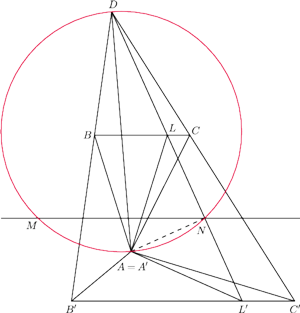
Przypadek 2. W trójkącie
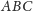 żaden bok nie ma takiej samej
długości jak bok
trójkąta
żaden bok nie ma takiej samej
długości jak bok
trójkąta
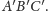 Bez utraty ogólności rozważań przyjmujemy,
że
Bez utraty ogólności rozważań przyjmujemy,
że
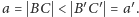 Umieszczamy trójkąty
Umieszczamy trójkąty
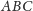 i
i
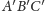 tak, że mają one wspólny wierzchołek
tak, że mają one wspólny wierzchołek
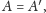 boki
boki
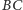 i
i
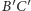 są równoległe i punkt
są równoległe i punkt
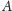 należy do pasa
wyznaczonego przez proste zawierające te odcinki. Niech
należy do pasa
wyznaczonego przez proste zawierające te odcinki. Niech
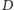 będzie
punktem przecięcia prostych
będzie
punktem przecięcia prostych
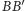 i
i
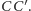
Na odcinku
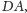 jako na średnicy, wykreślamy okrąg
jako na średnicy, wykreślamy okrąg
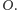 Prosta
przechodząca przez środki boków
Prosta
przechodząca przez środki boków
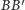 i
i
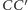 przecina ten okrąg
w punktach
przecina ten okrąg
w punktach
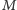 i
i
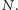 Wówczas prosta
Wówczas prosta
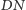 przecina odcinek
przecina odcinek
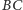 w punkcie
w punkcie
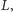 a odcinek
a odcinek
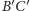 w punkcie
w punkcie
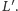 Punkty
Punkty
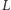 i
i
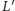 dzielą odcinki
dzielą odcinki
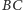 i
i
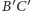 w takim samym
stosunku, na mocy twierdzenia Talesa. Zatem pole trójkąta
w takim samym
stosunku, na mocy twierdzenia Talesa. Zatem pole trójkąta
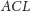 stanowi
taką samą część pola trójkąta
stanowi
taką samą część pola trójkąta
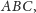 jaką częścią pola trójkąta
jaką częścią pola trójkąta
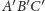 jest pole trójkąta
jest pole trójkąta
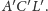 Ponieważ pola trójkątów
Ponieważ pola trójkątów
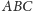 i
i
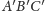 są równe, więc równe są też pola trójkątów
są równe, więc równe są też pola trójkątów
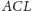 i
i
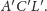
Ponadto, ponieważ
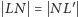 i kąt
i kąt
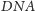 jest prosty,
więc
jest prosty,
więc
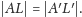 Umieszczamy teraz trójkąty
Umieszczamy teraz trójkąty
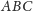 i
i
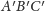 tak, by odcinki
tak, by odcinki
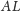 i
i
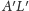 leżały na prostej
leżały na prostej
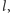 a wierzchołki
a wierzchołki
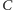 i
i
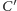 leżały w tej samej półpłaszczyźnie.
Z równości pól trójkątów
leżały w tej samej półpłaszczyźnie.
Z równości pól trójkątów
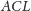 i
i
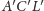 wynika, że
wierzchołki
wynika, że
wierzchołki
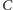 i
i
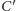 leżą na prostej
leżą na prostej
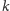 równoległej do
równoległej do
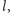 a wierzchołki
a wierzchołki
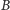 i
i
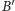 na prostej
na prostej
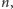 także
równoległej do
także
równoległej do
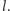
Dwukrotne odwołanie do przypadku 1 kończy dowód twierdzenia.