Stowarzyszenie na rzecz Edukacji Matematycznej
O zawodach II stopnia LXII Olimpiady matematycznej
W zawodach II stopnia LXII Olimpiady Matematycznej wzięło udział 599 uczniów z całej Polski. Spośród nich do finału zakwalifikowano 139 osób.
Oto jeden z problemów, z którymi przyszło im się zmierzyć:
Zadanie. Punkty
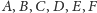 leżą w tej kolejności na
półokręgu o środku
leżą w tej kolejności na
półokręgu o środku
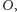 przy czym
przy czym
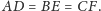 Cięciwa
Cięciwa
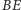 przecina cięciwy
przecina cięciwy
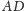 i
i
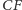 odpowiednio
w punktach
odpowiednio
w punktach
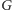 i
i
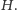 Wykazać, że
Wykazać, że

Jedną z metod używanych do dowodu tej równości było obrócenie układu
punktów
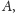
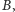
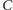 i
i
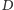 o kąt
o kąt
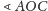 wokół
środka
wokół
środka
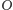 i stąd wnioskowanie o kątach. Przedstawimy jedno
z najładniejszych rozwiązań tego typu. Opiera się ono na pracy ucznia
Krzysztofa Kleinera z V LO im. Augusta Witkowskiego w Krakowie.
i stąd wnioskowanie o kątach. Przedstawimy jedno
z najładniejszych rozwiązań tego typu. Opiera się ono na pracy ucznia
Krzysztofa Kleinera z V LO im. Augusta Witkowskiego w Krakowie.
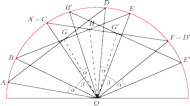
Rozwiązanie. Bez straty ogólności możemy
założyć, że promień danego okręgu wynosi 1. Będziemy używać
łukowych miar kątów, tzn.
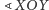 ma miarę równą długości łuku
ma miarę równą długości łuku
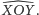 Ponieważ
Ponieważ
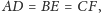 więc
więc
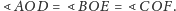 W takim razie
W takim razie

Analogicznie

Oznaczmy, jak na rysunku,
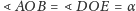 oraz
oraz
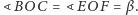 Mamy wtedy
Mamy wtedy

Obróćmy płaszczyznę o kąt
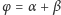 wokół
punktu
wokół
punktu
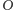 zgodnie z ruchem wskazówek zegara i oznaczmy obraz
dowolnego punktu
zgodnie z ruchem wskazówek zegara i oznaczmy obraz
dowolnego punktu
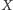 przez
przez
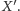 W szczególności mamy
W szczególności mamy
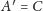 i
i
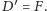 Punkt
Punkt
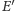 leży na okręgu, choć
– być może – poza danym półokręgiem. Mamy wtedy następujące
równości kątów:
leży na okręgu, choć
– być może – poza danym półokręgiem. Mamy wtedy następujące
równości kątów:

Oznaczmy
przez
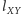 prostą zawierającą punkty
prostą zawierającą punkty
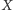 i
i
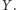 Ponieważ
Ponieważ
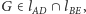 więc
więc
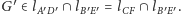 Zauważmy
teraz, że ośmiokąt
Zauważmy
teraz, że ośmiokąt
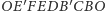 jest przystający do figury
jest przystający do figury
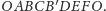 Istnieje zatem izometria płaszczyzny
przekształcająca punkty
Istnieje zatem izometria płaszczyzny
przekształcająca punkty
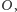
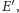
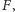
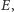
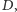
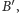
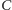 i
i
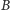 odpowiednio na punkty
odpowiednio na punkty
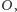
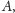
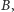
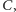
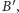
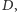
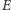 i
i
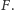 Zatem obrazem prostej
Zatem obrazem prostej
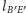 jest prosta
jest prosta
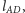 prostej
prostej
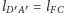 – prosta
– prosta
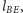 a prostej
a prostej
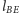 – prosta
– prosta
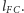 W takim razie: punkt
W takim razie: punkt
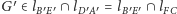 przechodzi na
przechodzi na
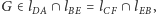 a punkt
a punkt
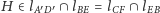 na siebie.
na siebie.
Stąd wynika równość
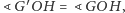 a z niej:
a z niej:

czego chcieliśmy dowieść.
Uwaga. Izometria, o której mowa w rozwiązaniu, to symetria względem prostej
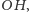 bo jest to złożenie obrotu o kąt
bo jest to złożenie obrotu o kąt
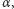 przeciwnie do ruchu
wskazówek zegara, wokół punktu
przeciwnie do ruchu
wskazówek zegara, wokół punktu
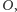 z symetrią osiową względem
prostej
z symetrią osiową względem
prostej
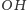 i jeszcze raz z tym samym obrotem.
i jeszcze raz z tym samym obrotem.