Sprawa niezbyt pedagogiczna
Richard Feynman, laureat Nagrody Nobla z fizyki, miał bardzo krytyczny stosunek do rozważań czysto teoretycznych. Wspomina o tym Kai Lai Chung, wybitny probabilista amerykański, w książce Green, Brown and Probability.
Feynman wypowiadał się o eternal futility nie tylko matematyki wyższej, ale również teoretycznej fizyki i astronomii. Twierdził, że matematycy są niepotrzebni, bo gdy fizykowi jakiś wynik matematyczny będzie potrzebny, to sam potrafi go udowodnić. Wiedząc o tym, Chung postanowił z Feynmana zażartować i podczas spotkania w restauracji zaproponował mu udowodnienie następującego twierdzenia geometrycznego.
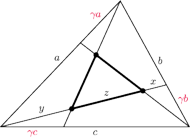
Twierdzenie. Boki trójkąta dzielimy na trzy równe części, a następnie
łączymy odcinkami każdy z wierzchołków z pierwszym punktem podziału
na przeciwległym boku. W rezultacie odcinki utworzą trójkąt, którego pole
jest równe
 pola wyjściowego trójkąta.
pola wyjściowego trójkąta.
Feynman przyjął ten fakt z niedowierzaniem i po kilku obliczeniach stwierdził, że twierdzenie nie jest prawdziwe, bo wskazują na to jego przybliżone obliczenia. Przyjął zakład, że ma rację, i poddał się dopiero wtedy, gdy stwierdził, że twierdzenie jest prawdziwe dla trójkąta równobocznego. W związku z tym zdarzeniem proponujemy kilka zadań.
Zadanie 1. Udowodnić sformułowane powyżej twierdzenie
- a)
- dla trójkąta równobocznego,
- b)
- dla trójkąta dowolnego.
Zadanie 2. Na bokach trójkąta zaznaczamy punkty w odległości od
wierzchołków równej
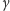 razy długość boku, gdzie
razy długość boku, gdzie
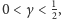 i łączymy je odcinkami z przeciwległymi wierzchołkami.
Jaki jest stosunek pól
i łączymy je odcinkami z przeciwległymi wierzchołkami.
Jaki jest stosunek pól
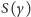 trójkąta utworzonego z odcinków
i wyjściowego trójkąta?
trójkąta utworzonego z odcinków
i wyjściowego trójkąta?
Zadanie 3 (Kontynuacja zadania 2). Znaleźć wszystkie takie
liczby naturalne
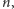 że gdy
że gdy
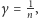 to stosunek pól jest postaci
to stosunek pól jest postaci
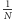 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej
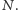
Zadanie 4 (Kontynuacja zadania 3). Znaleźć wszystkie takie wymierne
liczby
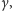 że
że
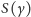 jest również liczbą wymierną.
jest również liczbą wymierną.
Zadanie 5. Czy dla czworokątów prawdziwe jest twierdzenie analogiczne do twierdzenia przedstawionego Feynmanowi?
Zadanie 6 (Kontynuacja zadania 2).
Wyznaczyć długości odcinków
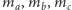 łączących wierzchołki
z zaznaczonymi punktami w zależności od liczby
łączących wierzchołki
z zaznaczonymi punktami w zależności od liczby
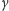 i długości
boków trójkąta
i długości
boków trójkąta
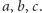
Podpowiedzi.
-
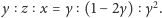
-
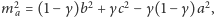
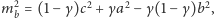
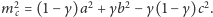
- Niech
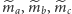 będą długościami boków otrzymanego
trójkąta. Wtedy
będą długościami boków otrzymanego
trójkąta. Wtedy
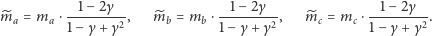
- Niech
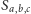 oznacza pole trójkąta o bokach
oznacza pole trójkąta o bokach
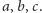 Udowodnić, że
Udowodnić, że
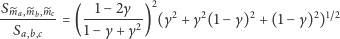
(
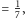 gdy
gdy
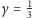 ).
).
[Kai Lai Chung, Green, Brown and Probability, World Scientific, 1995.]