Izogonalnie sprzężone
Tym razem o elipsie w zadaniach olimpijskich.
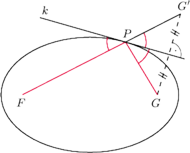
Rys. 1 Prosta
 – styczna do elipsy w punkcie
– styczna do elipsy w punkcie
 , punkt
, punkt
 – obraz
– obraz
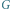 w symetrii względem
w symetrii względem
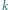 . Wtedy punkty
. Wtedy punkty
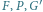 leżą na jednej prostej i
leżą na jednej prostej i
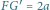 .
.
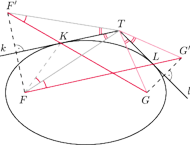
Rys. 2
Definicja. Elipsa o ogniskach w punktach
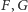 i o stałej
i o stałej
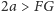 to zbiór takich punktów
to zbiór takich punktów
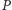 płaszczyzny,
że
płaszczyzny,
że
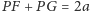 .
.
W poprzednim deltoidzie udowodniliśmy kilka własności elips (m.in. Rys. 1). W tym numerze wykorzystamy elipsy do rozwiązania zadań olimpijskich. Zacznijmy od jeszcze kilku własności.
Fakt 1. Z punktu
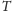 poprowadzono proste
poprowadzono proste
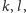 styczne do elipsy
o ogniskach
styczne do elipsy
o ogniskach
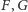 odpowiednio w punktach
odpowiednio w punktach
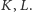 Wówczas
Wówczas
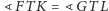 i
i
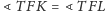 .
.
Dowód. Niech
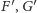 będą obrazami ognisk
będą obrazami ognisk
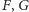 w symetriach odpowiednio względem
prostych
w symetriach odpowiednio względem
prostych
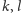 (Rys. 2). Wtedy
(Rys. 2). Wtedy
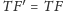 ,
,
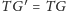 oraz, z rysunku 1,
oraz, z rysunku 1,
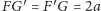 .
Wobec tego
.
Wobec tego
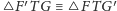 , zatem
, zatem
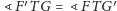 . Stąd
równość kątów
. Stąd
równość kątów
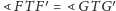 , czyli też ich połówek:
, czyli też ich połówek:
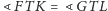 .
.
Kolejno z symetrii, ze współliniowości punktów
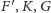 ,
z przystawania
,
z przystawania
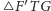 i
i
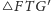 oraz ze współliniowości
punktów
oraz ze współliniowości
punktów
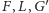 , mamy
, mamy
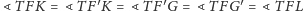 .
.
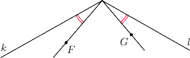
Ćwiczenia. Udowodnij, że:
- a) dla dowolnych punktów
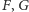 , izogonalnie sprzężonych
względem danych prostych
, izogonalnie sprzężonych
względem danych prostych
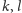 (rysunek obok), istnieje
elipsa o ogniskach
(rysunek obok), istnieje
elipsa o ogniskach
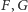 styczna do tych prostych,
styczna do tych prostych,
- b) jeśli punkty
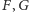 wewnątrz trójkąta są
izogonalnie sprzężone względem każdej z dwóch par prostych
zawierających boki, to są też sprzężone względem trzeciej pary,
wewnątrz trójkąta są
izogonalnie sprzężone względem każdej z dwóch par prostych
zawierających boki, to są też sprzężone względem trzeciej pary,
- c) takie
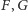 są wtedy ogniskami pewnej elipsy wpisanej
w ten trójkąt,
są wtedy ogniskami pewnej elipsy wpisanej
w ten trójkąt,
- d) w dowolny trójkąt ostrokątny można wpisać
elipsę o ogniskach
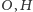 , gdzie
, gdzie
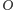 to środek okręgu
opisanego, a
to środek okręgu
opisanego, a
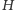 to ortocentrum trójkąta.
to ortocentrum trójkąta.
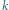 – styczna do elipsy w punkcie
– styczna do elipsy w punkcie
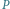 , punkt
, punkt
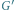 – obraz
– obraz
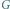 w symetrii względem
w symetrii względem
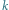 . Wtedy punkty
. Wtedy punkty
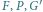 leżą na jednej prostej i
leżą na jednej prostej i
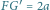 .
.