Deltoid
Dobrze się składa
Jednokładności były tematem styczniowego deltoidu. Jak każde przekształcenia, jednokładności można składać. Mimo, że wynik takiego złożenia nie musi być jednokładnością, to jednak jednokładności składają się dobrze.
Przypomnijmy, że jednokładność o środku
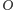 i skali
i skali
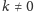 to
przekształcenie geometryczne płaszczyzny, które punktowi
to
przekształcenie geometryczne płaszczyzny, które punktowi
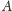 przypisuje
punkt
przypisuje
punkt
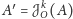 spełniający warunek
spełniający warunek
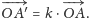
Fakt.
Dla nieprzystających okręgów
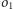 i
i
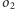 istnieje dokładnie jedna
jednokładność taka, że
istnieje dokładnie jedna
jednokładność taka, że
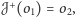 oraz dokładnie jedna taka,
że
oraz dokładnie jedna taka,
że
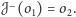
Zachodzi następujące miłe twierdzenie, dowód pozostawiam jako zadanie.
Twierdzenie. Złożenie dwóch jednokładności jest albo jednokładnością
o skali będącej iloczynem wyjściowych skal i środku współliniowym ze
środkami składanych jednokładności, albo przesunięciem, jeśli iloczyn
wyjściowych skal jest równy
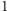 .
.
Skoro jednokładności tak dobrze się składa, zobaczmy kilka zastosowań.
Poniższe zadanie pochodzi z L Olimpiady Matematycznej.