O tym, czego nie ma

Wzory na pierwiastki wielomianu stopnia 5

Każdy uczeń szkoły średniej wie, że gdy zna się współczynniki trójmianu kwadratowego, to można jawnymi wzorami wyrazić pierwiastki tego trójmianu. We wzorach tych wykonuje się (skończoną liczbę razy) tylko cztery działania arytmetyczne i pierwiastkowanie.

Podobnie rzecz się ma z wielomianami stopnia trzeciego i czwartego. Są wzory (bardziej zawiłe niż w przypadku trójmianu kwadratowego) wyrażające pierwiastki takiego wielomianu poprzez jego współczynniki.

Od niemal 200 lat wiadomo (Ruffini, Abel, Galois), że nie ma wzorów pozwalających wyrazić pierwiastki wielomianu stopnia większego od 4 jako funkcje współczynników tego wielomianu, o ile chcemy ograniczyć się do wykonywania (skończoną liczbę razy!) tylko czterech działań arytmetycznych i wyciągania pierwiastków różnych stopni. To twierdzenie o nieistnieniu nie powinno przerażać inżyniera, który przypadkiem natrafi na równanie stopnia piątego. Istnieją bowiem znakomite sposoby (np. metoda stycznych Newtona), które pozwalają na przybliżone znajdowanie pierwiastków takiego równania z dowolną z góry określoną dokładnością.

Kto przeszedł przez podstawowy kurs analizy matematycznej, słyszał zapewne, że całki nieoznaczonej 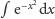$\text{[math]}$ nie można wyrazić przez funkcje elementarne za pomocą skończonej liczby działań arytmetycznych i składania funkcji, bez stosowania przejścia do granicy. To twierdzenie niewiele różni się od twierdzenia Ruffiniego–Abela–Galoisa, w tym sensie przynajmniej, że oba twierdzenia mają dowody korzystające z tych samych metod.