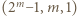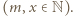Wykażemy, że równanie nie ma rozwiązań, w których 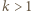 oraz
oraz 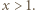 Z tożsamości
Z tożsamości
wynika spostrzeżenie:
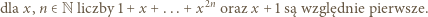 |
(1) |
Stąd wniosek, że rozważane równanie nie może być spełnione, gdy 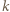 jest liczbą parzystą.
jest liczbą parzystą.
Gdy 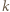 jest liczbą nieparzystą postaci
jest liczbą nieparzystą postaci 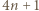 (
( 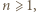 bo rozważamy
bo rozważamy 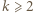 ), zapisujemy lewą stronę równania jako iloczyn
), zapisujemy lewą stronę równania jako iloczyn 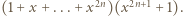 Prawa strona równania, równa
Prawa strona równania, równa 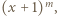 musiałaby się dzielić przez
musiałaby się dzielić przez 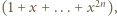 co nie jest możliwe, znów w myśl uwagi (1).
co nie jest możliwe, znów w myśl uwagi (1).
Gdy natomiast 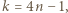 mnożymy równanie stronami przez
mnożymy równanie stronami przez 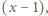 otrzymując
otrzymując
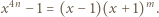 |
(2) |
Lewa strona dzieli się przez 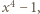 więc i przez
więc i przez 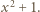 Liczba
Liczba 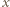 nie może być parzysta, bo wówczas liczba
nie może być parzysta, bo wówczas liczba 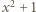 byłaby względnie pierwsza z oboma czynnikami prawej strony (2). Niech więc
byłaby względnie pierwsza z oboma czynnikami prawej strony (2). Niech więc 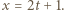 Skoro lewa (więc i prawa) strona (2) dzieli się przez
Skoro lewa (więc i prawa) strona (2) dzieli się przez 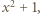 możemy napisać
możemy napisać 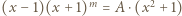
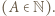 Po podstawieniu
Po podstawieniu 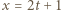 wychodzi
wychodzi
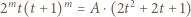 |
(3) |
- sprzeczność, bo liczba w nawiasie po prawej stronie (3) jest względnie pierwsza z każdym z czynników lewej strony (3).
Pozostają sytuacje trywialne, gdy 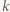 lub
lub 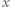 równa się 1. Jeśli
równa się 1. Jeśli 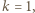 to
to 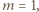 zaś
zaś 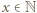 może być dowolne. A gdy
może być dowolne. A gdy 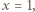 równanie mówi jedynie, że
równanie mówi jedynie, że 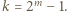 Tak więc wszystkimi rozwiązaniami równania są trójki
Tak więc wszystkimi rozwiązaniami równania są trójki 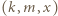 postaci
postaci 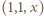 lub
lub 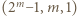
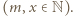
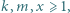 spełniające równanie
spełniające równanie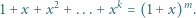

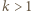 oraz
oraz 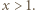 Z tożsamości
Z tożsamości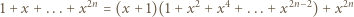
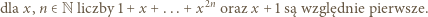
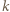 jest liczbą parzystą.
jest liczbą parzystą.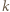 jest liczbą nieparzystą postaci
jest liczbą nieparzystą postaci 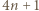 (
( 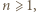 bo rozważamy
bo rozważamy 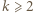 ), zapisujemy lewą stronę równania jako iloczyn
), zapisujemy lewą stronę równania jako iloczyn 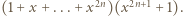 Prawa strona równania, równa
Prawa strona równania, równa 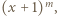 musiałaby się dzielić przez
musiałaby się dzielić przez 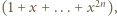 co nie jest możliwe, znów w myśl uwagi (1).
co nie jest możliwe, znów w myśl uwagi (1).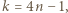 mnożymy równanie stronami przez
mnożymy równanie stronami przez 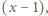 otrzymując
otrzymując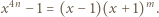
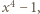 więc i przez
więc i przez 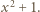 Liczba
Liczba 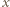 nie może być parzysta, bo wówczas liczba
nie może być parzysta, bo wówczas liczba 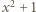 byłaby względnie pierwsza z oboma czynnikami prawej strony (2). Niech więc
byłaby względnie pierwsza z oboma czynnikami prawej strony (2). Niech więc 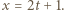 Skoro lewa (więc i prawa) strona (2) dzieli się przez
Skoro lewa (więc i prawa) strona (2) dzieli się przez 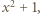 możemy napisać
możemy napisać 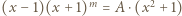
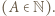 Po podstawieniu
Po podstawieniu 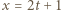 wychodzi
wychodzi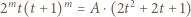
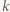 lub
lub 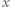 równa się 1. Jeśli
równa się 1. Jeśli 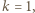 to
to 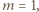 zaś
zaś 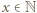 może być dowolne. A gdy
może być dowolne. A gdy 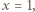 równanie mówi jedynie, że
równanie mówi jedynie, że 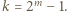 Tak więc wszystkimi rozwiązaniami równania są trójki
Tak więc wszystkimi rozwiązaniami równania są trójki 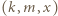 postaci
postaci 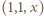 lub
lub