Klub 44M - zadania I 2018»Zadanie 754
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2018
- Publikacja w Delcie: styczeń 2018
- Publikacja elektroniczna: 1 stycznia 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (102 KB)
-
Zadanie 754 zaproponował pan Mikołaj Pater.
Znaleźć wszystkie trójki liczb rzeczywistych 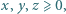 spełniające układ równań
spełniające układ równań
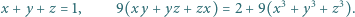

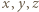 będą liczbami nieujemnymi, spełniającymi podany układ równań. Ich suma, więc i jej kwadrat, wynosi 1; wobec tego
będą liczbami nieujemnymi, spełniającymi podany układ równań. Ich suma, więc i jej kwadrat, wynosi 1; wobec tego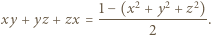
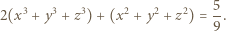
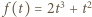 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale 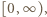 zatem spełnia nierówność Jensena
zatem spełnia nierówność Jensena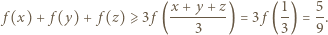
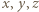 ) nierówność (2) staje się równością, co ma miejsce jedynie, gdy te liczby są równe. Ich suma jest jedynką, więc
) nierówność (2) staje się równością, co ma miejsce jedynie, gdy te liczby są równe. Ich suma jest jedynką, więc 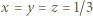 ; ta trójka liczb spełnia oba równania układu i stanowi jego jedyne rozwiązanie.
; ta trójka liczb spełnia oba równania układu i stanowi jego jedyne rozwiązanie.