Zadanie ZM-14.11-zadania-4
o zadaniu...
- Publikacja w Delcie: listopad 2014
- Publikacja elektroniczna: 31-10-2014
Niech 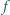 będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli
będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli  i
i 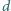 są różnymi liczbami całkowitymi, to
są różnymi liczbami całkowitymi, to  dzieli
dzieli 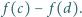

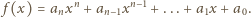
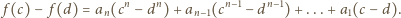
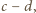 zatem suma
zatem suma 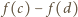 jest także podzielna przez
jest także podzielna przez 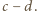
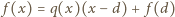 dla pewnego wielomianu
dla pewnego wielomianu 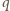 (którego współczynniki także są całkowite). Stąd
(którego współczynniki także są całkowite). Stąd 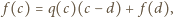 czyli
czyli 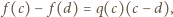 gdzie
gdzie 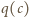 jest liczbą całkowitą.
jest liczbą całkowitą.