Zadanie ZM-1617
o zadaniu...
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
Niech 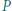 będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień
będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień 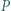 wynosi 1.
wynosi 1.

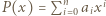 spełnia warunki zadania. Zauważmy, że możemy wybrać
spełnia warunki zadania. Zauważmy, że możemy wybrać 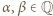 takie, że wielomian
takie, że wielomian 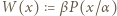 ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech
ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech 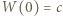 i niech
i niech 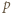 będzie liczbą pierwszą. Jeśli
będzie liczbą pierwszą. Jeśli 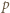 jest dostatecznie duże, to równanie
jest dostatecznie duże, to równanie 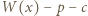 ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie
ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie 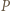 jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko
jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko 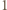 lub
lub 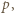 zatem dla dostatecznie dużych
zatem dla dostatecznie dużych 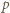 musi to być
musi to być 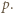 Wynika stąd, że
Wynika stąd, że 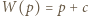 dla dostatecznie dużych liczb pierwszych
dla dostatecznie dużych liczb pierwszych 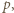 zatem
zatem 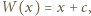 co oznacza, że
co oznacza, że 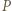 jest stopnia 1.
jest stopnia 1.