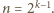Matematyka jest jedna: wielomiany mogą wszystko»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Matematyka jest jedna: wielomiany mogą wszystko
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
Niech 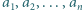 oraz
oraz 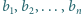 będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci
będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci 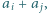 gdzie
gdzie 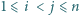 pokrywa się z zestawem
pokrywa się z zestawem 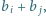 dla
dla 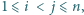 to
to 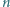 jest potęgą liczby 2.
jest potęgą liczby 2.


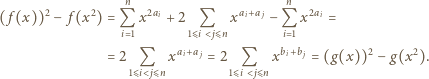
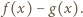 Nie jest to wielomian zerowy oraz
Nie jest to wielomian zerowy oraz 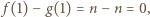 a więc liczba
a więc liczba 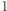 jest jego pierwiastkiem. Oznaczmy przez
jest jego pierwiastkiem. Oznaczmy przez 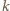 krotność owego pierwiastka, czyli
krotność owego pierwiastka, czyli 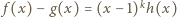 dla pewnego wielomianu
dla pewnego wielomianu 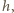 takiego, że
takiego, że 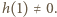 Wówczas
Wówczas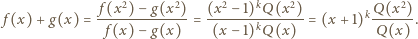
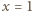 w powyższej równości, dostajemy
w powyższej równości, dostajemy