Zadanie ZM-1557
o zadaniu...
- Publikacja w Delcie: luty 2018
- Publikacja elektroniczna: 1 lutego 2018
Dane są liczby całkowite 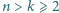 oraz tablica
oraz tablica 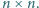 Wyróżniono
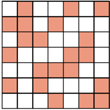
Wyróżniono 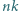 pól tej tablicy w taki sposób, że w każdym wierszu i w każdej kolumnie jest dokładnie
pól tej tablicy w taki sposób, że w każdym wierszu i w każdej kolumnie jest dokładnie 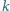 wyróżnionych pól, a ponadto każda para kolumn tej tablicy ma w dokładnie jednym wierszu obydwa pola wyróżnione (np. jak na rysunku). Udowodnić, że każda para wierszy tej tablicy ma w dokładnie jednej kolumnie obydwa pola wyróżnione.
wyróżnionych pól, a ponadto każda para kolumn tej tablicy ma w dokładnie jednym wierszu obydwa pola wyróżnione (np. jak na rysunku). Udowodnić, że każda para wierszy tej tablicy ma w dokładnie jednej kolumnie obydwa pola wyróżnione.

![A= [a ] i j](/math/temat/matematyka/algebra/zadania/2018/01/28/zm-1557/1x-269812c355b2430697c88bed5f9fdc71b1d00f6c-im-66,57,43-FF,FF,FF.gif) wymiarów
wymiarów 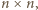 w której
w której 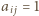 jeżeli pole o współrzędnych
jeżeli pole o współrzędnych 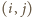 danej tablicy jest wyróżnione oraz
danej tablicy jest wyróżnione oraz 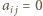 w przeciwnym przypadku. Wówczas
w przeciwnym przypadku. Wówczas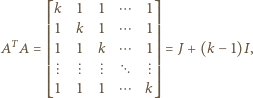
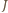 oraz
oraz 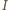 to odpowiednio macierz jedynek oraz macierz identyczności wymiarów
to odpowiednio macierz jedynek oraz macierz identyczności wymiarów 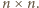 Łatwo sprawdzić, że dla
Łatwo sprawdzić, że dla 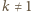 macierz
macierz 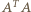 jest nieosobliwa, skąd wynika, że również macierz
jest nieosobliwa, skąd wynika, że również macierz 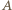 jest nieosobliwa. Wobec tego
jest nieosobliwa. Wobec tego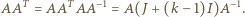
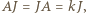 skąd wobec powyższej równości mamy
skąd wobec powyższej równości mamy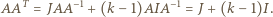
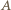 ma iloczyn skalarny równy
ma iloczyn skalarny równy 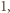 co w myśl definicji macierzy
co w myśl definicji macierzy 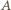 kończy dowód.
kończy dowód.