Zadanie

Narzędzia
Obiekty: Liczby pierwsze, Rachunki
Słowa kluczowe
Kategoria: Algebra

Szły raz drogą trzy sześciany»Zadanie 10

o zadaniu...

Zadanie pochodzi z artykułu Szły raz drogą trzy sześciany
Publikacja w Delcie: styczeń 2020
Publikacja elektroniczna: 31 grudnia 2019
Artykuł źródłowy w wersji do druku [application/pdf]: (377 KB)

Dana jest liczba pierwsza 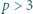$p > 3$ oraz takie liczby całkowite dodatnie 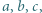$|a,b,c,$ że

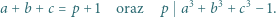3 3 3 a+ b +c = p +1 oraz p a + b + c − 1.

Dowieść, że co najmniej jedna z liczb 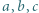$a,b, c$ jest równa 1.

Wskazówka

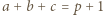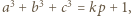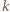W równości (1) z artykułu podstawić $a +b + c = p + 1$ i $a3 + b3 + c3 = kp + 1,$ gdzie $k$ jest jakąś liczbą całkowitą. Wywnioskować stąd, że 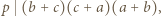$|p (b + c)(c+ a)(a + b),$ więc któryś z czynników dzieli się przez 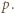$p.$ Te czynniki są dodatnie i nie przekraczają 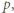$p,$ więc któryś z nich jest równy $|p.$