Podróże w 
Jakiś czas temu koleżanki i koledzy z redakcji Delty poprosili mnie, żebym opisał, czym zajmuję się naukowo, i przedstawił pewien ciekawy wynik, który udało mi się wraz ze współpracownikami niedawno uzyskać. Pisząc ten tekst, postaram się przybliżyć tę właśnie dziedzinę, która mi osobiście wydaje się interesująca chyba dlatego, że rozważa problemy o bardzo prostym sformułowaniu geometrycznym, a mimo to jest w niej więcej znaków zapytania niż odpowiedzi. Badania często okazują się ciekawą kombinatoryką, popartą jednak zwykle geometrycznymi intuicjami. Wiele fundamentalnych pytań otwartych można sformułować bardzo szybko, jedno z nich przybliżę na końcu tego tekstu.
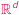
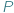 w sumie algebraicznej
w sumie algebraicznej 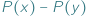 można wyłączyć przed nawias wyrażenie
można wyłączyć przed nawias wyrażenie 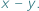
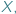 np.
np. 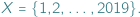 Niech
Niech 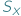 oznacza zbiór funkcji odwracalnych z
oznacza zbiór funkcji odwracalnych z 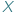 w
w  Funkcje z
Funkcje z 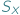 można składać i odwracać, nie wychodząc poza
można składać i odwracać, nie wychodząc poza 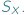 W zbiorze
W zbiorze 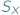 istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru
istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru 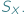
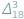 (Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
(Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...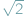 jest niewymierne, czyli że dla żadnej liczby naturalnej
jest niewymierne, czyli że dla żadnej liczby naturalnej 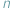 liczba
liczba 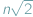 nie jest całkowita.
nie jest całkowita.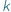 -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru 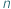 -elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez
-elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez 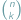 (symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
(symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...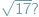 Odpowiedź brzmi: tak.
Odpowiedź brzmi: tak.
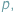 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 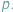 Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.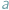
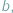


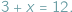 Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie
Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 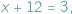 które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...
które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...