- Narzędzia
- Obiekty
- Liczby rzeczywiste , Wielomiany
- Słowa kluczowe
- Kategoria
- Algebra
Matematyka jest jedna: wielomiany mogą wszystko»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Matematyka jest jedna: wielomiany mogą wszystko
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
Udowodnić, że liczba

jest niewymierna.
Rozwiązanie
Oznaczmy sumę daną w zadaniu przez 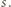 Udowodnimy najpierw, że liczba
Udowodnimy najpierw, że liczba  nie jest całkowita. Zauważmy w tym celu, że dla dowolnej liczby całkowitej
nie jest całkowita. Zauważmy w tym celu, że dla dowolnej liczby całkowitej 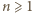 zachodzą nierówności
zachodzą nierówności

Pierwsza z nich jest oczywista, zaś druga po podniesieniu do kwadratu redukuje się do

co jest prawdą, gdyż 
W szczególności dla dowolnego 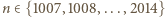 prawdziwe są nierówności
prawdziwe są nierówności

Wynika stąd, że suma  nie jest liczbą całkowitą, gdyż część ułamkowa każdego z jej
nie jest liczbą całkowitą, gdyż część ułamkowa każdego z jej 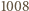 składników jest mniejsza niż
składników jest mniejsza niż 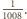 Dowodzi to naszego stwierdzenia.
Dowodzi to naszego stwierdzenia.
Może się wydawać, że do osiągnięcia celu jest jeszcze daleko. Liczba, która nie jest całkowita, nie musi przecież od razu być niewymierna. W tym jednak momencie można zacząć podejrzewać, jaką rolę odegrają własności wielomianów. W następnym kroku udowodnimy bowiem, że istnieje wielomian unormowany 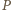 o współczynnikach całkowitych, taki, że
o współczynnikach całkowitych, taki, że 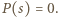 Stąd już natychmiast otrzymamy tezę zadania, gdyż z twierdzenia o pierwiastku wymiernym wynika, że każdy wymierny pierwiastek wielomianu
Stąd już natychmiast otrzymamy tezę zadania, gdyż z twierdzenia o pierwiastku wymiernym wynika, że każdy wymierny pierwiastek wielomianu 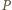 jest również całkowity. W szczególności, skoro
jest również całkowity. W szczególności, skoro 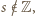 to tym samym
to tym samym 
Za pomocą indukcji po  wykażemy ogólniejsze stwierdzenie: dla dowolnych liczb całkowitych
wykażemy ogólniejsze stwierdzenie: dla dowolnych liczb całkowitych 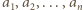 istnieje unormowany wielomian
istnieje unormowany wielomian 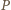 o współczynnikach całkowitych, dla którego
o współczynnikach całkowitych, dla którego

Gdy 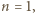 wystarczy przyjąć
wystarczy przyjąć 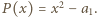 Załóżmy więc, że
Załóżmy więc, że 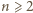 oraz istnieje wielomian unormowany
oraz istnieje wielomian unormowany 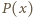 o współczynnikach całkowitych, dla którego
o współczynnikach całkowitych, dla którego 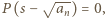 gdzie
gdzie 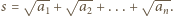 Przyjmijmy, że stopień wielomianu
Przyjmijmy, że stopień wielomianu 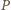 to
to  i że
i że 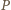 zapisuje się w postaci
zapisuje się w postaci 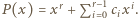 W szczególności
W szczególności

Po rozwinięciu wszystkich potęg ze wzoru dwumianowego Newtona otrzymujemy równanie postaci

gdzie 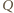 i
i 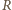 są wielomianami o współczynnikach całkowitych stopnia mniejszego niż
są wielomianami o współczynnikach całkowitych stopnia mniejszego niż 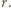 Przenosząc składnik
Przenosząc składnik 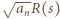 na drugą stronę i podnosząc obie strony równości do kwadratu, dostajemy
na drugą stronę i podnosząc obie strony równości do kwadratu, dostajemy

W szczególności liczba  jest pierwiastkiem unormowanego wielomianu
jest pierwiastkiem unormowanego wielomianu

Kończy to zarówno dowód indukcyjny, jak i rozwiązanie zadania.
Uwaga
Twierdzenie (O pierwiastku wymiernym). Jeżeli liczba wymierna 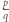 (zapisana w postaci nieskracalnej) jest pierwiastkiem wielomianu
(zapisana w postaci nieskracalnej) jest pierwiastkiem wielomianu

o współczynnikach całkowitych, to 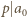 oraz
oraz 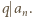 W szczególności, jeżeli współczynnik wiodący wielomianu
W szczególności, jeżeli współczynnik wiodący wielomianu 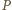 jest równy
jest równy 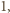 to dowolny pierwiastek tego wielomianu, który jest liczbą wymierną, jest również liczbą całkowitą.
to dowolny pierwiastek tego wielomianu, który jest liczbą wymierną, jest również liczbą całkowitą.
