Niech 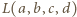 oznacza lewą stronę podanego równania, pomnożoną przez
oznacza lewą stronę podanego równania, pomnożoną przez 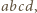 i niech
i niech 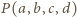 oznacza prawą stronę tego równania, pomnożoną przez
oznacza prawą stronę tego równania, pomnożoną przez 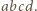 Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np.
Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np. 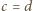 :
:
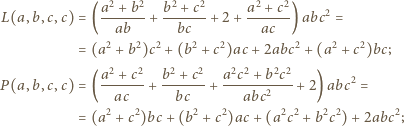
te wartości są równe. To znaczy, że wielomian 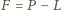 dzieli się przez dwumian
dzieli się przez dwumian 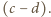 Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany
Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany 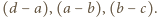 Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby
Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby 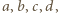 stwierdzamy, że ta stała to 1. Tak więc
stwierdzamy, że ta stała to 1. Tak więc
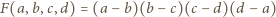
(oczywiście można było tę tożsamość sprawdzić wprost, podstawiając wyrażenie określające rozważane działanie, przenosząc wszystko na jedną stronę i pracowicie przekształcając).
Dane w zadaniu równanie 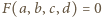 nie jest spełnione dla żadnej czwórki różnych liczb
nie jest spełnione dla żadnej czwórki różnych liczb 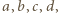 jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
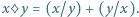 Niech
Niech 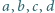 będą liczbami, spełniającymi równanie
będą liczbami, spełniającymi równanie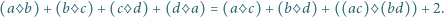
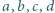 mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?
mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?
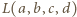 oznacza lewą stronę podanego równania, pomnożoną przez
oznacza lewą stronę podanego równania, pomnożoną przez 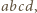 i niech
i niech 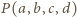 oznacza prawą stronę tego równania, pomnożoną przez
oznacza prawą stronę tego równania, pomnożoną przez 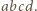 Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np.
Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np. 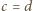 :
: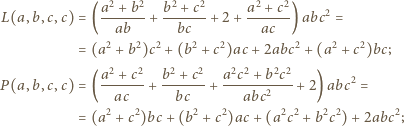
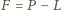 dzieli się przez dwumian
dzieli się przez dwumian 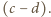 Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany
Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany 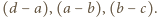 Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby
Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby 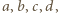 stwierdzamy, że ta stała to 1. Tak więc
stwierdzamy, że ta stała to 1. Tak więc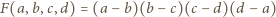
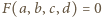 nie jest spełnione dla żadnej czwórki różnych liczb
nie jest spełnione dla żadnej czwórki różnych liczb 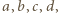 jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).