Klub 44M - zadania VI 2014»Zadanie 684
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2014
- Publikacja w Delcie: czerwiec 2014
- Publikacja elektroniczna: 2 czerwca 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (89 KB)
-
Zadanie 684 zaproponował pan Tomasz Ordowski.
Wykazać, że dla żadnej pary różnych liczb pierwszych 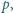
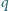 układ równań
układ równań
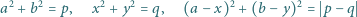
nie ma rozwiązań w liczbach całkowitych 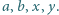

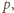
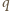 oraz
oraz 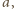
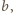
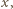
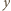 spełniają podane warunki. Można przyjąć, że
spełniają podane warunki. Można przyjąć, że 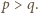 Odejmując pierwsze równanie od drugiego i uwzględniając równanie trzecie, dostajemy związek
Odejmując pierwsze równanie od drugiego i uwzględniając równanie trzecie, dostajemy związek 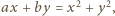 czyli
czyli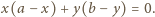
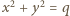 jest liczbą pierwszą, zatem liczby
jest liczbą pierwszą, zatem liczby 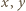 są względnie pierwsze i żadna z nich nie jest zerem. Z równania (1) wynika teraz, że
są względnie pierwsze i żadna z nich nie jest zerem. Z równania (1) wynika teraz, że  jest dzielnikiem różnicy
jest dzielnikiem różnicy 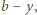 zaś
zaś 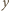 jest dzielnikiem różnicy
jest dzielnikiem różnicy  Tak więc
Tak więc 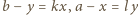 dla pewnych liczb całkowitych
dla pewnych liczb całkowitych 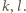 Po podstawieniu do równania (1) mamy
Po podstawieniu do równania (1) mamy 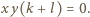 Ale
Ale 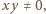 więc
więc 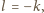 i dalej:
i dalej: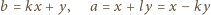
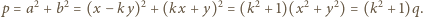
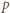 taka równość zachodzić nie może. Sprzeczność dowodzi, że liczby o podanych własnościach nie istnieją.
taka równość zachodzić nie może. Sprzeczność dowodzi, że liczby o podanych własnościach nie istnieją.