Klub 44M - zadania VI 2018»Zadanie 763
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2018
- Publikacja w Delcie: czerwiec 2018
- Publikacja elektroniczna: 22 maja 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (89 KB)
Dany jest wielomian 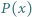 stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna
stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna 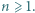 Udowodnić, że może istnieć co najwyżej jeden wielomian
Udowodnić, że może istnieć co najwyżej jeden wielomian 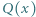 stopnia
stopnia 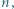 spełniający równanie
spełniający równanie 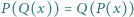 dla
dla 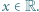

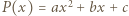
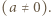 Przypuśćmy, że dla ustalonej liczby
Przypuśćmy, że dla ustalonej liczby 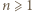 istnieją dwa różne wielomiany
istnieją dwa różne wielomiany 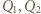 stopnia
stopnia 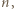 spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez
spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez 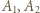 (więc
(więc 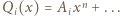 );
); 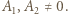 Przyrównując współczynniki wiodące po obu stronach równania
Przyrównując współczynniki wiodące po obu stronach równania 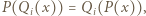 widzimy, że
widzimy, że 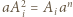 (dla
(dla 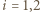 ). Zatem
). Zatem 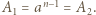 Stąd wynika, że różnica
Stąd wynika, że różnica 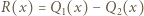 jest niezerowym wielomianem stopnia
jest niezerowym wielomianem stopnia 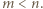
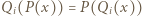 (dla
(dla 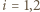 ) i przekształcamy uzyskaną równość:
) i przekształcamy uzyskaną równość: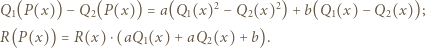
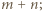 wielomian po lewej stronie ma stopień
wielomian po lewej stronie ma stopień 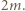 To już sprzeczność, skoro
To już sprzeczność, skoro 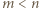 ; dwa różne wielomiany
; dwa różne wielomiany 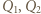 stopnia
stopnia 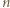 o podanej własności istnieć nie mogą.
o podanej własności istnieć nie mogą.