Przykładami wielomianów, o jakich mowa, stopni 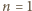 oraz
oraz 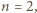 mogą być
mogą być 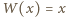 oraz
oraz 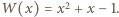 Wykażemy, że nie istnieje wielomian o podanych własnościach, stopnia
Wykażemy, że nie istnieje wielomian o podanych własnościach, stopnia 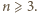
Przypuśćmy, że 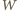 jest takim wielomianem. Zestaw wszystkich
jest takim wielomianem. Zestaw wszystkich 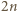 pierwiastków wielomianu
pierwiastków wielomianu 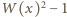 rozdzielamy na ciąg
rozdzielamy na ciąg 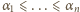 pierwiastków wielomianu
pierwiastków wielomianu 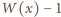 oraz ciąg
oraz ciąg 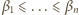 pierwiastków wielomianu
pierwiastków wielomianu 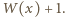 Wówczas
Wówczas
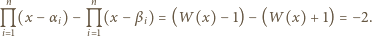 |
(1) |
Podstawiając 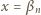 mamy
mamy 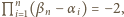 skąd wynika, że najmniejszy z czynników tego iloczynu jest liczbą ujemną:
skąd wynika, że najmniejszy z czynników tego iloczynu jest liczbą ujemną: 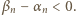 Wobec tego
Wobec tego 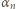 jest liczbą większą od wszystkich
jest liczbą większą od wszystkich 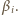 Widzimy ponadto, że liczby
Widzimy ponadto, że liczby 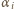 nie mogą być wszystkie równe, bo liczba
nie mogą być wszystkie równe, bo liczba 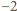 nie jest iloczynem
nie jest iloczynem 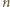 równych liczb całkowitych. Zatem
równych liczb całkowitych. Zatem 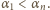
Podstawiając z kolei w równaniu (1) 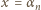 dostajemy
dostajemy 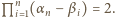 Jest to iloczyn dodatnich liczb całkowitych; największa musi być dwójką, a pozostałe jedynkami - to znaczy,
Jest to iloczyn dodatnich liczb całkowitych; największa musi być dwójką, a pozostałe jedynkami - to znaczy,
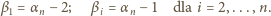 |
(2) |
Wracamy do równania (1) i podstawiamy 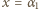 ; otrzymujemy równość
; otrzymujemy równość 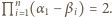 Zgodnie ze wzorami (2), przepisujemy ją w postaci
Zgodnie ze wzorami (2), przepisujemy ją w postaci
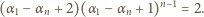 |
(3) |
Skoro 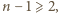 czynnik
czynnik 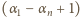 musi być równy
musi być równy 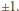 Gdyby był równy
Gdyby był równy 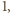 znaczyłoby to, że
znaczyłoby to, że 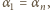 wbrew wcześniejszemu spostrzeżeniu. Gdyby był równy
wbrew wcześniejszemu spostrzeżeniu. Gdyby był równy 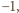 w pierwszym nawiasie wzoru (3) mielibyśmy
w pierwszym nawiasie wzoru (3) mielibyśmy 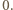 Równość (3) doprowadziła do sprzeczności.
Równość (3) doprowadziła do sprzeczności.
Wielomiany o postulowanych własnościach istnieją więc tylko dla 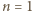 i
i 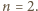 (Nietrudno znaleźć ich ogólną postać - zostawiamy to jako ćwiczenie).
(Nietrudno znaleźć ich ogólną postać - zostawiamy to jako ćwiczenie).
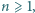 dla których istnieje wielomian
dla których istnieje wielomian 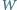 stopnia
stopnia 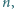 o współczynnikach całkowitych, ze współczynnikiem wiodącym równym 1, i taki, że równanie
o współczynnikach całkowitych, ze współczynnikiem wiodącym równym 1, i taki, że równanie 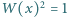 ma
ma 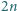 pierwiastków całkowitych (niekoniecznie różnych).
pierwiastków całkowitych (niekoniecznie różnych).
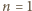 oraz
oraz 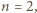 mogą być
mogą być 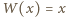 oraz
oraz 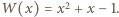 Wykażemy, że nie istnieje wielomian o podanych własnościach, stopnia
Wykażemy, że nie istnieje wielomian o podanych własnościach, stopnia 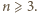
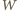 jest takim wielomianem. Zestaw wszystkich
jest takim wielomianem. Zestaw wszystkich 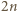 pierwiastków wielomianu
pierwiastków wielomianu 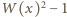 rozdzielamy na ciąg
rozdzielamy na ciąg 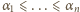 pierwiastków wielomianu
pierwiastków wielomianu 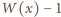 oraz ciąg
oraz ciąg 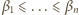 pierwiastków wielomianu
pierwiastków wielomianu 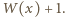 Wówczas
Wówczas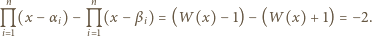
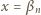 mamy
mamy 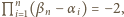 skąd wynika, że najmniejszy z czynników tego iloczynu jest liczbą ujemną:
skąd wynika, że najmniejszy z czynników tego iloczynu jest liczbą ujemną: 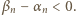 Wobec tego
Wobec tego 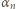 jest liczbą większą od wszystkich
jest liczbą większą od wszystkich 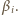 Widzimy ponadto, że liczby
Widzimy ponadto, że liczby 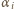 nie mogą być wszystkie równe, bo liczba
nie mogą być wszystkie równe, bo liczba 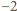 nie jest iloczynem
nie jest iloczynem 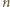 równych liczb całkowitych. Zatem
równych liczb całkowitych. Zatem 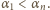
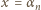 dostajemy
dostajemy 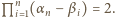 Jest to iloczyn dodatnich liczb całkowitych; największa musi być dwójką, a pozostałe jedynkami - to znaczy,
Jest to iloczyn dodatnich liczb całkowitych; największa musi być dwójką, a pozostałe jedynkami - to znaczy,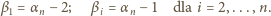
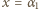 ; otrzymujemy równość
; otrzymujemy równość 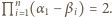 Zgodnie ze wzorami (2), przepisujemy ją w postaci
Zgodnie ze wzorami (2), przepisujemy ją w postaci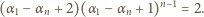
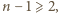 czynnik
czynnik 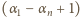 musi być równy
musi być równy 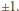 Gdyby był równy
Gdyby był równy 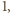 znaczyłoby to, że
znaczyłoby to, że 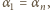 wbrew wcześniejszemu spostrzeżeniu. Gdyby był równy
wbrew wcześniejszemu spostrzeżeniu. Gdyby był równy 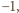 w pierwszym nawiasie wzoru (3) mielibyśmy
w pierwszym nawiasie wzoru (3) mielibyśmy 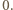 Równość (3) doprowadziła do sprzeczności.
Równość (3) doprowadziła do sprzeczności.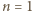 i
i 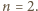 (Nietrudno znaleźć ich ogólną postać - zostawiamy to jako ćwiczenie).
(Nietrudno znaleźć ich ogólną postać - zostawiamy to jako ćwiczenie).