Zadanie

Narzędzia
Obiekty: Liczby naturalne, Wielomiany
Słowa kluczowe
Kategoria: Algebra

Twierdzenie Bézouta»Zadanie 3

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Bézouta
Publikacja w Delcie: grudzień 2019
Publikacja elektroniczna: 30 listopada 2019
Artykuł źródłowy w wersji do druku [application/pdf]: (374 KB)

Wielomian 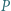$P$ o współczynnikach całkowitych przyjmuje wartość 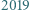$|2019$ dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.

Wskazówka

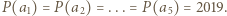Niech $P (a1) = P(a2) = ... = P(a5) = 2019.$ Liczby 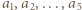$a1,a2,...,a5$ są różnymi pierwiastkami wielomianu 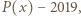$P (x) −2019,$ więc na mocy twierdzenia Bézouta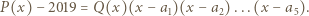

P(x) − 2019 = Q(x)(x

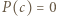Gdyby $|P(c) = 0$ dla pewnego całkowitego 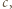$|c,$ to liczba $2019$ byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.