Klub 44M - zadania II 2015»Zadanie 695
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2015
- Publikacja w Delcie: luty 2015
- Publikacja elektroniczna: 1 lutego 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (125 KB)
Znaleźć wszystkie pary wielomianów rzeczywistych 
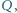 spełniające równanie
spełniające równanie
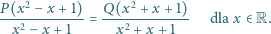

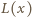 oraz
oraz 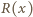 lewą i prawą stronę postulowanego równania
lewą i prawą stronę postulowanego równania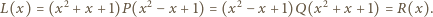
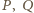 nie są wielomianami zerowymi. Jasne, że muszą mieć jednakowy stopień
nie są wielomianami zerowymi. Jasne, że muszą mieć jednakowy stopień 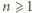 oraz równe współczynniki wiodące:
oraz równe współczynniki wiodące: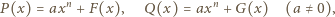
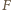 i
i 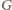 są wielomianami stopni co najwyżej
są wielomianami stopni co najwyżej 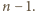 Tak więc
Tak więc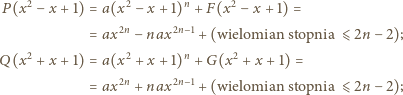
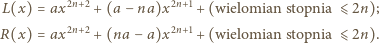
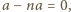 czyli
czyli 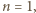 czyli
czyli 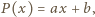
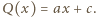 Podstawiając w wyjściowym równaniu
Podstawiając w wyjściowym równaniu 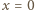 oraz
oraz 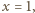 otrzymujemy zależności
otrzymujemy zależności 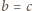 oraz
oraz 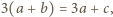 skąd
skąd 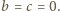 Ostatecznie więc
Ostatecznie więc 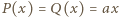 ; przyjęliśmy, że
; przyjęliśmy, że 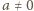 - wszelako dla
- wszelako dla 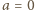 dostajemy parę wielomianów zerowych, które też są rozwiązaniem. Oczywiście każda para postaci
dostajemy parę wielomianów zerowych, które też są rozwiązaniem. Oczywiście każda para postaci 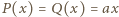
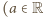 - dowolna stała) spełnia zadane równanie.
- dowolna stała) spełnia zadane równanie.