Zadanie

Narzędzia
Obiekty: Liczby pierwsze, Wielomiany
Słowa kluczowe
Kategoria: Algebra

Twierdzenie Bézouta»Zadanie 7

o zadaniu...

Zadanie pochodzi z artykułu Twierdzenie Bézouta
Publikacja w Delcie: grudzień 2019
Publikacja elektroniczna: 30 listopada 2019
Artykuł źródłowy w wersji do druku [application/pdf]: (374 KB)

Wielomian 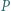$P$ o współczynnikach całkowitych ma tę własność, że 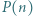$|P(n)$ jest liczbą pierwszą dla wszystkich naturalnych 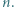$n.$ Dowieść, że 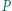$|P$ jest wielomianem stałym.

Wskazówka

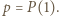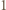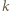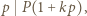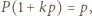Niech $|p = P (1).$ Na mocy twierdzenia $1$ dla naturalnych $|k$ mamy $|p P (1+ kp),$ więc $P(1 +kp) = p,$ gdyż wartości 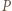$P$ dla argumentów całkowitych są liczbami pierwszymi. Wielomian 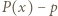$P(x) − p$ ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.