- Narzędzia
- Obiekty
- Wielomiany
- Słowa kluczowe
- Kategoria
- Algebra
Matematyka jest jedna: wielomiany mogą wszystko»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Matematyka jest jedna: wielomiany mogą wszystko
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
Rozważmy zbiór

złożony z 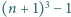 punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór
punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór 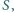 ale nie zawiera punktu
ale nie zawiera punktu 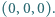
Rozwiązanie
Zauważmy, że 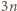 płaszczyzn o równaniach
płaszczyzn o równaniach 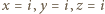 dla
dla 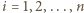 spełnia żądany warunek. Wykażemy, że
spełnia żądany warunek. Wykażemy, że 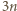 jest minimalną liczbą o tej własności.
jest minimalną liczbą o tej własności.
Załóżmy więc, że suma mnogościowa pewnych 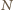 płaszczyzn danych równaniami
płaszczyzn danych równaniami

pokrywa zbiór 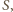 ale nie zawiera punktu
ale nie zawiera punktu 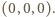 Rozważmy wielomian trzech zmiennych
Rozważmy wielomian trzech zmiennych 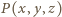 dany jako
dany jako

Jest to wielomian łącznego stopnia 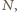 który spełnia warunek
który spełnia warunek 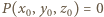 dla
dla 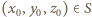 oraz
oraz 
Za pomocą wielomianu 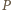 udało się nam przetłumaczyć kombinatoryczny warunek dotyczący płaszczyzn na język algebry. Dzięki temu możemy wykorzystać jej narzędzia, zapominając o kombinatorycznej naturze zadania.
udało się nam przetłumaczyć kombinatoryczny warunek dotyczący płaszczyzn na język algebry. Dzięki temu możemy wykorzystać jej narzędzia, zapominając o kombinatorycznej naturze zadania.
Dla dowolnego wielomianu trzech zmiennych 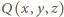 określmy operację
określmy operację 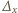 zdefiniowaną jako
zdefiniowaną jako

W analogiczny sposób definiujemy operację 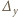 oraz
oraz 
Za pomocą nietrudnego rachunku na współczynnikach sprawdzimy najpierw, że operacja 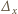 zmniejsza łączny stopień wielomianu co najmniej o
zmniejsza łączny stopień wielomianu co najmniej o 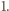 Załóżmy bowiem, że stopień pewnego wielomianu
Załóżmy bowiem, że stopień pewnego wielomianu 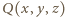 to
to 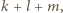 przy czym w rozwinięciu
przy czym w rozwinięciu 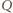 pojawia się jednomian postaci
pojawia się jednomian postaci 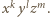 Korzystając ze wzoru dwumianowego Newtona, uzyskujemy
Korzystając ze wzoru dwumianowego Newtona, uzyskujemy

Otrzymaliśmy więc sumę jednomianów o łącznym stopniu nieprzekraczającym 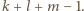 Stosując to samo rozumowanie do każdego jednomianu postaci
Stosując to samo rozumowanie do każdego jednomianu postaci 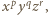 który pojawia się w rozwinięciu
który pojawia się w rozwinięciu 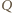 i spełnia
i spełnia 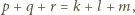 widzimy, że operacja
widzimy, że operacja 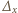 redukuje wszystkie jednomiany o łącznym stopniu
redukuje wszystkie jednomiany o łącznym stopniu 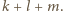 Potwierdza to nasze stwierdzenie.
Potwierdza to nasze stwierdzenie.
Zauważmy, że skoro wielomian 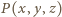 zeruje się dla dowolnej trójki
zeruje się dla dowolnej trójki 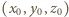 spełniającej
spełniającej 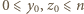 oraz
oraz 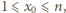 to
to 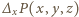 zeruje się dla dowolnej trójki
zeruje się dla dowolnej trójki 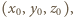 która spełnia
która spełnia 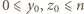 oraz
oraz 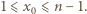 Jednocześnie, mamy
Jednocześnie, mamy

Powtarzając operację 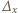 aż
aż 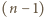 -krotnie, otrzymujemy wielomian
-krotnie, otrzymujemy wielomian 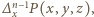 który zeruje się dla dowolnej trójki postaci
który zeruje się dla dowolnej trójki postaci 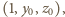 gdzie
gdzie 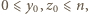 oraz nie zeruje się dla
oraz nie zeruje się dla 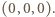 Używając więc operacji
Używając więc operacji 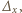 już ostatni raz dostajemy
już ostatni raz dostajemy

Wielomian, który otrzymaliśmy z wielomianu 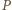 po
po  -krotnym zastosowaniu operacji
-krotnym zastosowaniu operacji 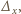 nie zeruje się więc w punkcie
nie zeruje się więc w punkcie 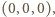 ale zeruje się dla dowolnego punktu postaci
ale zeruje się dla dowolnego punktu postaci 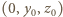 gdzie
gdzie 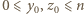 i co najmniej jedna z liczb
i co najmniej jedna z liczb 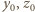 jest różna od zera.
jest różna od zera.
Możemy zatem powtórzyć cały powyższy proces, tym razem względem zmiennej 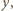 startując od wielomianu otrzymanego w ostatnim kroku. Wielomian
startując od wielomianu otrzymanego w ostatnim kroku. Wielomian 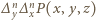 zeruje się więc dla dowolnej trójki postaci
zeruje się więc dla dowolnej trójki postaci 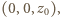 gdzie
gdzie 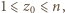 ale nie dla trójki
ale nie dla trójki 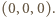 Ostatecznie już, rozumując w ten sam sposób względem zmiennej
Ostatecznie już, rozumując w ten sam sposób względem zmiennej 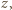 dochodzimy do wniosku, że wielomian
dochodzimy do wniosku, że wielomian 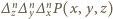 nie zeruje się w punkcie
nie zeruje się w punkcie 
Nie jest to zatem wielomian zerowy. Wcześniej udowodniliśmy jednak, że dowolna z operacji 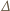 redukuje łączny stopień wielomianu co najmniej o
redukuje łączny stopień wielomianu co najmniej o 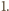 Stopień wielomianu
Stopień wielomianu 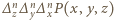 nie przekracza zatem
nie przekracza zatem 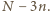 Stąd
Stąd 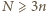 i rozwiązanie zadania jest zakończone.
i rozwiązanie zadania jest zakończone.
