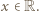Gdy 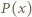 jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że
jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że 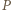 jest wielomianem stopnia dodatniego. Wielomian
jest wielomianem stopnia dodatniego. Wielomian 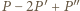 ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian
ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian 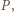 jak i wielomian
jak i wielomian 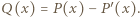 Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę
Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę  przy
przy  przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc
przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc
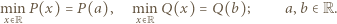
W punkcie, realizującym minimum, pochodna jest równa zeru: 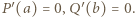 Zauważmy, że, w myśl założenia zadania,
Zauważmy, że, w myśl założenia zadania,
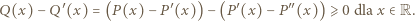
Podstawiając 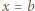 dostajemy
dostajemy 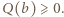 Jest to wartość minimalna wielomianu
Jest to wartość minimalna wielomianu 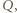 zatem
zatem
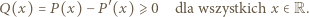
Podstawiamy 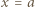 i mamy
i mamy 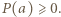 To wartość minimalna wielomianu
To wartość minimalna wielomianu 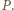 Zatem
Zatem 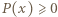 dla
dla 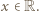
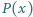 będzie takim wielomianem o współczynnikach rzeczywistych, że
będzie takim wielomianem o współczynnikach rzeczywistych, że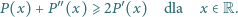
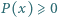 dla
dla 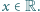

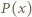 jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że
jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że 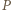 jest wielomianem stopnia dodatniego. Wielomian
jest wielomianem stopnia dodatniego. Wielomian 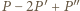 ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian
ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian 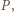 jak i wielomian
jak i wielomian 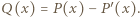 Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę
Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę  przy
przy  przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc
przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc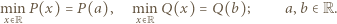
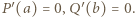 Zauważmy, że, w myśl założenia zadania,
Zauważmy, że, w myśl założenia zadania,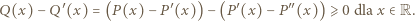
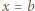 dostajemy
dostajemy 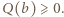 Jest to wartość minimalna wielomianu
Jest to wartość minimalna wielomianu 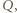 zatem
zatem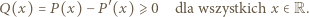
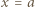 i mamy
i mamy 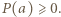 To wartość minimalna wielomianu
To wartość minimalna wielomianu 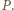 Zatem
Zatem 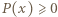 dla
dla