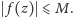O tym, czego nie ma
Wielomian, który nie ma pierwiastków
Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie
algebry, udowodnione przez Carla Friedricha Gaussa w ostatnim roku
osiemnastego stulecia, informuje nas, że pewne obiekty nie istnieją.
Mianowicie, nie ma takiego, różnego od stałej, wielomianu zmiennej
zespolonej, który nie znikałby w żadnym punkcie płaszczyzny zespolonej
Dziś znanych jest wiele dowodów zasadniczego twierdzenia algebry, chciałoby się rzec, jeden piękniejszy od drugiego. Żaden, niestety, nie nadaje się do tego, by zwięźle i ze wszystkimi niezbędnymi szczegółami przedstawić go Czytelnikom Delty. Dla ciekawych – szkic dwóch różnych dowodów nie korzystających wcale z metod algebraicznych.
Pierwszy dowód zasadniczego twierdzenia algebry
Dowód opiera się na dwóch lematach, z których zasadnicze twierdzenie algebry wynika natychmiast.
Dowód. Wystarczy zauważyć, że dla punktów
 leżących poza dużym kołem domkniętym
leżących poza dużym kołem domkniętym
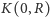 moduł
wielomianu jest duży, zatem kresy dolne zbiorów
moduł
wielomianu jest duży, zatem kresy dolne zbiorów
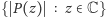 i
i
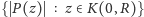 są równe. Funkcja
są równe. Funkcja
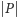 jest ciągła, więc
na zwartym zbiorze
jest ciągła, więc
na zwartym zbiorze
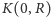 osiąga swój kres dolny.
osiąga swój kres dolny.
Lemat 2. Niech
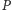 będzie wielomianem niezerowego stopnia. Jeśli
będzie wielomianem niezerowego stopnia. Jeśli
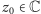 jest takim punktem, że
jest takim punktem, że
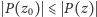 dla wszystkich
dla wszystkich
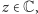 to wtedy
to wtedy
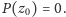
Dowód tego lematu jest trudniejszy i znacznie bardziej techniczny, lecz można go przeprowadzić dysponując jedynie elementarną wiedzą o liczbach zespolonych.
Dowód. Najprościej jest dokonać reductio ad absurdum a robi
się to tak. Mnożąc w razie potrzeby wielomian przez stałą i przesuwając
jego wykres, można założyć, że
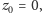
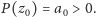 Przypuśćmy też, że wielomian
Przypuśćmy też, że wielomian
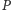 nie zawiera dodatnich potęg
nie zawiera dodatnich potęg
 mniejszych od
mniejszych od
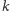 -tej,
-tej,
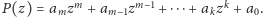 Zatem
Zatem
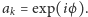 Wtedy, dla
Wtedy, dla
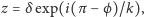 mamy
mamy
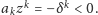 Zatem
Zatem
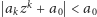 dla małych
dla małych
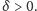 Nietrudno teraz wykazać,
że dopisanie pod modułem pozostałych wyrazów wielomianu nic nie
popsuje: jest ich skończenie wiele i wszystkie są blisko zera nieskończenie
mniej ważne niż
Nietrudno teraz wykazać,
że dopisanie pod modułem pozostałych wyrazów wielomianu nic nie
popsuje: jest ich skończenie wiele i wszystkie są blisko zera nieskończenie
mniej ważne niż
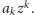 Dokładny dobór
Dokładny dobór
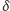 zostawiamy
wytrwałym Czytelnikom.
zostawiamy
wytrwałym Czytelnikom.
Drugi dowód zasadniczego twierdzenia algebry
Ten dowód wykorzystuje tzw.
Twierdzenie (Liouville’a). Załóżmy, że
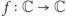 jest funkcją
ograniczoną. Jeśli
jest funkcją
ograniczoną. Jeśli
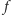 jest różniczkowalna w każdym punkcie,
tzn. dla każdego
jest różniczkowalna w każdym punkcie,
tzn. dla każdego
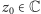 istnieje granica
istnieje granica

to
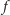 jest tożsamościowo równa pewnej stałej.
jest tożsamościowo równa pewnej stałej.
Dowód tego faktu można znaleźć w dowolnym podręczniku teorii
funkcji zmiennej zespolonej. Warto zauważyć, że gdy liczby zespolone
zastąpić rzeczywistymi, to twierdzenie Liouville’a będzie fałszywe (przykład:
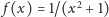 ).
).
Dowód zasadniczego twierdzenia algebry.
Przypuśćmy teraz, że
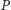 jest takim wielomianem zmiennej
zespolonej, że
jest takim wielomianem zmiennej
zespolonej, że
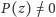 dla wszystkich
dla wszystkich
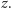 Nietrudno wtedy
zauważyć, że funkcja
dana wzorem
Nietrudno wtedy
zauważyć, że funkcja
dana wzorem
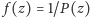 spełnia wszystkie założenia twierdzenia
Liouville’a (ograniczoność funkcji
spełnia wszystkie założenia twierdzenia
Liouville’a (ograniczoność funkcji
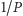 wynika, podobnie jak
Lemat 1 w pierwszym dowodzie, z obserwacji, że moduł wielomianu
nie może być mały na zewnątrz pewnego dużego koła). Zatem,
wynika, podobnie jak
Lemat 1 w pierwszym dowodzie, z obserwacji, że moduł wielomianu
nie może być mały na zewnątrz pewnego dużego koła). Zatem,
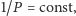 a więc także
a więc także
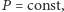 co kończy dowód.
co kończy dowód.
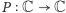
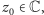
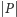
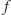 jest ograniczona, jeśli istnieje taka liczba
jest ograniczona, jeśli istnieje taka liczba
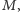 że dla wszystkich zespolonych
że dla wszystkich zespolonych
 mamy
mamy