O tym, czego nie ma
Dlaczego w przestrzeni trójwymiarowej nie ma przyzwoitego mnożenia?
Płaszczyznę
 można wyposażyć w działania dodawania i
mnożenia jej punktów. Dlaczego nie można tego zrobić z przestrzenią
można wyposażyć w działania dodawania i
mnożenia jej punktów. Dlaczego nie można tego zrobić z przestrzenią
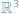 ?
?
Wszyscy uczyliśmy się w szkole dodawać i mnożyć liczby rzeczywiste. Łatwo wymienić podstawowe własności tych działań:
- (a)
- dodawanie jest łączne, przemienne i ma element neutralny; dla
każdego elementu
 istnieje element przeciwny
istnieje element przeciwny
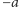 ;
;
- (b)
- mnożenie jest łączne, przemienne i ma element neutralny
 ; dla
każdego elementu
; dla
każdego elementu
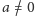 istnieje element odwrotny
istnieje element odwrotny
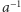 ;
;
- (c)
- mnożenie jest rozdzielne względem dodawania.
Oprócz zbioru liczb rzeczywistych
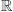 w szkole poznaliśmy też zbiory liczb
naturalnych
w szkole poznaliśmy też zbiory liczb
naturalnych
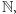 całkowitych
całkowitych
 i wymiernych
i wymiernych
 Chociaż
w każdym z nich możemy liczby dodawać i mnożyć, tylko
Chociaż
w każdym z nich możemy liczby dodawać i mnożyć, tylko
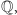 obok
obok
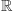 , spełnia wszystkie wymagania (a)–(c). Matematyk powie krótko,
że zbiory
, spełnia wszystkie wymagania (a)–(c). Matematyk powie krótko,
że zbiory
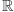 i
i
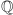 są ciałami, a zbiory
są ciałami, a zbiory
 i
i
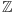 ciałami
nie są.
ciałami
nie są.
Przykładem ciała większego od
 jest zbiór liczb zespolonych
jest zbiór liczb zespolonych
 Przypomnijmy, że liczbami zespolonymi nazywamy wyrażenia postaci
Przypomnijmy, że liczbami zespolonymi nazywamy wyrażenia postaci
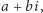 gdzie
gdzie
 Liczby te dodajemy i mnożymy podobnie
jak wielomiany z wykorzystaniem dodatkowej relacji:
Liczby te dodajemy i mnożymy podobnie
jak wielomiany z wykorzystaniem dodatkowej relacji:
 Nietrudno
sprawdzić, że tak określone działania mają własności (a)–(c), tj.
Nietrudno
sprawdzić, że tak określone działania mają własności (a)–(c), tj.
 jest ciałem.
jest ciałem.
Ponieważ każda liczba zespolona
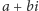 jest w istocie parą
liczb rzeczywistych
jest w istocie parą
liczb rzeczywistych
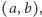 zbiór
zbiór
 możemy uznać za
płaszczyznę
możemy uznać za
płaszczyznę
 wyposażoną w działania dodawania i mnożenia jej
punktów. Przy powyższej interpretacji działania te wyrażają się wzorami
wyposażoną w działania dodawania i mnożenia jej
punktów. Przy powyższej interpretacji działania te wyrażają się wzorami
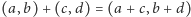 oraz
oraz
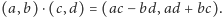
Zauważmy, że powyższe dodawanie można łatwo uogólnić na przestrzeń
trójwymiarową
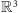 : należy trójki liczb dodawać jak wektory,
tj. „ po współrzędnych”
: należy trójki liczb dodawać jak wektory,
tj. „ po współrzędnych”

Powstaje ciekawe pytanie: czy przestrzeń trójwymiarową
 można
wyposażyć dodatkowo w działanie mnożenia, które by wraz z takim
dodawaniem spełniało warunki (a)–(c)? Chcielibyśmy przy tym, by to
mnożenie było też zgodne z istniejącym w
można
wyposażyć dodatkowo w działanie mnożenia, które by wraz z takim
dodawaniem spełniało warunki (a)–(c)? Chcielibyśmy przy tym, by to
mnożenie było też zgodne z istniejącym w
 mnożeniem przez
skalary, tj. aby zachodziły równości
mnożeniem przez
skalary, tj. aby zachodziły równości
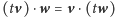 dla dowolnych
dla dowolnych
 oraz
oraz
 O takim mnożeniu mówimy, że jest
dwuliniowe.
O takim mnożeniu mówimy, że jest
dwuliniowe.
Udowodnimy
Twierdzenie. W przestrzeni
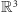 nie istnieje mnożenie, które by
wraz z dodawaniem „po współrzędnych” spełniało warunki (a)–(c).
nie istnieje mnożenie, które by
wraz z dodawaniem „po współrzędnych” spełniało warunki (a)–(c).
Dowód poprowadzimy nie wprost. Przypuśćmy, że przestrzeń
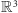 ma takie mnożenie. O elementach
ma takie mnożenie. O elementach
 będzie nam wygodnie
myśleć, jak o wektorach zaczepionych w punkcie
będzie nam wygodnie
myśleć, jak o wektorach zaczepionych w punkcie
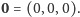
Z warunku (b) wynika, że jeden z wektorów jest jedynką mnożenia
– oznaczymy go przez
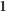 . Niech
. Niech
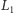 będzie prostą naciągniętą na tym
wektorze, tj.
będzie prostą naciągniętą na tym
wektorze, tj.
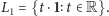 Dla dowolnego wektora
Dla dowolnego wektora
 oznaczmy przez
oznaczmy przez
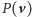 płaszczyznę naciągniętą na parze wektorów
płaszczyznę naciągniętą na parze wektorów
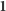 ,
,
 . Najpierw zauważmy, że zachodzi
. Najpierw zauważmy, że zachodzi
Lemat 1. Niech
 Jeśli jego kwadrat
Jeśli jego kwadrat
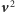 należy
do płaszczyzny
należy
do płaszczyzny
 to
to
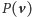 jest podzbiorem zamkniętym
względem dodawania, odejmowania, mnożenia i brania odwrotności.
jest podzbiorem zamkniętym
względem dodawania, odejmowania, mnożenia i brania odwrotności.
Dowód. Oczywiście, płaszczyzna zawierająca punkt
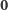 jest
zamknięta względem dodawania i odejmowania wektorów.
jest
zamknięta względem dodawania i odejmowania wektorów.
Każdy element
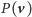 jest postaci
jest postaci
 dla pewnych
dla pewnych
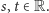 Kiedy pomnożymy dwa takie wyrażenia i otworzymy
nawiasy, otrzymamy kombinację wektorów
Kiedy pomnożymy dwa takie wyrażenia i otworzymy
nawiasy, otrzymamy kombinację wektorów
 ,
,
 ,
,
 Ponieważ każdy z nich leży w
Ponieważ każdy z nich leży w
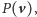 więc iloczyn naszych
wyrażeń też tam się znajdzie.
więc iloczyn naszych
wyrażeń też tam się znajdzie.
Pozostało wykazać, że jeśli
 oraz
oraz
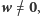 to
to
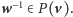 Jeśli
Jeśli
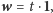 to
to
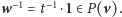 W przeciwnym przypadku
W przeciwnym przypadku
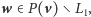 a zatem
a zatem
 Ponieważ wiemy już, że
Ponieważ wiemy już, że
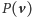 jest zamknięte względem mnożenia, to
jest zamknięte względem mnożenia, to
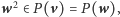 tj.
tj.
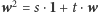 dla pewnych
dla pewnych

Jeśli jest
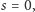 to
to
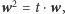 a zatem
a zatem
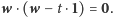 To jest jednak niemożliwe, ponieważ oba czynniki są różne od zera.
Mamy więc
To jest jednak niemożliwe, ponieważ oba czynniki są różne od zera.
Mamy więc
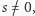 a stąd
a stąd
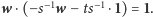
Zatem
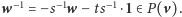
A teraz zauważymy, że sytuacja z poprzedniego lematu... nigdy nie zachodzi.
Dowód. Przypuśćmy, że
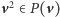 i weźmy dowolny
wektor
i weźmy dowolny
wektor
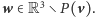 Wtedy wektory
Wtedy wektory
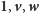 rozpinają całą
przestrzeń
rozpinają całą
przestrzeń
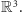 W szczególności, wektor
W szczególności, wektor
 może być
zapisany jako ich kombinacja:
może być
zapisany jako ich kombinacja:
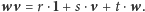 Ale wtedy
Ale wtedy
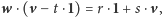 czyli
czyli
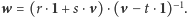 Z Lematu 1 wiemy, że wyrażenie
po prawej stronie należy do
Z Lematu 1 wiemy, że wyrażenie
po prawej stronie należy do
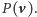 Zatem
Zatem
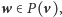 wbrew
założeniu.
wbrew
założeniu.
Dokończenie dowodu twierdzenia. Weźmy dowolny
wektor
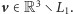 Z Lematu 2 wnosimy, że wektory
Z Lematu 2 wnosimy, że wektory
 rozpinają przestrzeń
rozpinają przestrzeń
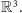 Zatem wektor
Zatem wektor
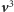 jest ich kombinacją:
jest ich kombinacją:
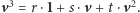
Rozważmy funkcję

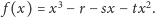 Ponieważ
Ponieważ
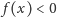 dla
wielkich liczb ujemnych oraz
dla
wielkich liczb ujemnych oraz
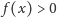 dla wielkich liczb dodatnich,
więc istnieje taka liczba
dla wielkich liczb dodatnich,
więc istnieje taka liczba
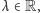 że
że
 Wobec tego mamy
tożsamość
Wobec tego mamy
tożsamość
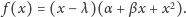 Podstawiając wektor
Podstawiając wektor
 w miejsce zmiennej
w miejsce zmiennej
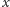 otrzymujemy
otrzymujemy

Z założenia oraz z Lematu 2 wynika, że obydwa czynniki są różne od zera. Otrzymana sprzeczność kończy dowód.
Uwaga dla koneserów: w dowodzie nie użyliśmy przemienności mnożenia.
A zatem przestrzeń
 nie ma nawet struktury nieprzemiennej algebry
z dzieleniem
nie ma nawet struktury nieprzemiennej algebry
z dzieleniem

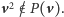
 i
i
 ?
?
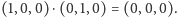 To w żadnym ciele się nie zdarza – dlaczego?
To w żadnym ciele się nie zdarza – dlaczego?
 ciała
ciała
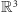 jest
jego podciałem.
jest
jego podciałem.