Rachunki
Fibonacci spotyka Banacha

Leonardo Fibonacci (1170-1240)
Fibonacci (właściwie Leonardo z Pizy, ok. 1170-1240) nauczył się zasad arytmetyki hindusko-arabskiej, gdy razem z ojcem przebywał w Bougie (obecnie algierska Bidżaja). Poszerzał swoją wiedzę podczas podróży do Egiptu, Syrii, Grecji, na Sycylię, do Prowansji. Gdy osiadł w Pizie, w 1202 roku napisał traktat Liber Abaci (Księga rachunków), z myślą o rozpowszechnieniu w Europie notacji dziesiętnej opartej na wykorzystaniu cyfr 0,1,2, ...,9. Pokazał w nim użyteczność nowych metod na wielu przykładach rachunkowych, szczególnie związanych z przeliczaniem miar i wag, obliczaniem zysków i odsetek, wymianą pieniędzy...
W 1225 roku napisał rozprawę Liber Quadratorum, która miała być kontynuacją Arytmetyki Diofantosa. Problemy rozważane przez Leonarda nie są banalne. Przekonujemy się o tym, rozwiązując zadania zamieszczone w jego tekstach:

Strona traktatu Liber abaci
Choć traktat Liber Abaci przyczynił się do rozwoju bankowości i rachunkowości w Europie, to największą sławę przyniósł Fibonacciemu niezwykły ciąg
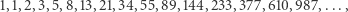 |
wykorzystany w rozwiązaniu zadania 4. Wcześniej, w VI wieku, ciąg ten został opisany przez matematyków hinduskich (Virahanka), ale wtedy nie wzbudził zainteresowania.
Definicja. Ciągiem Fibonacciego  o generatorach
o generatorach 
 nazywamy ciąg, którego kolejne wyrazy spełniają równość
nazywamy ciąg, którego kolejne wyrazy spełniają równość 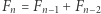 dla
dla 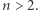
Ciągi z rodziny Fibonacciego (otrzymane dla różnych generatorów, przy rozmaitych modyfikacjach formuły na obliczanie wartości 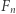 ) budzą wiele emocji u matematyków oraz miłośników matematyki rekreacyjnej. Dzieje się tak za sprawą odkrywania obecności ciągu Fibonacciego w naszym otoczeniu (np. w botanice), w sztuce - złota proporcja, w zastosowaniach ciągu Fibonacciego w teorii liczb. Nie wszystko o nim wiemy: w ciągu Fibonacciego występują liczby pierwsze
) budzą wiele emocji u matematyków oraz miłośników matematyki rekreacyjnej. Dzieje się tak za sprawą odkrywania obecności ciągu Fibonacciego w naszym otoczeniu (np. w botanice), w sztuce - złota proporcja, w zastosowaniach ciągu Fibonacciego w teorii liczb. Nie wszystko o nim wiemy: w ciągu Fibonacciego występują liczby pierwsze 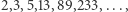 ale czy liczb pierwszych jest w nim nieskończenie wiele?
ale czy liczb pierwszych jest w nim nieskończenie wiele?
W 1611 roku Johannes Kepler w pracy Strena, Seu de Nive Sexangula, o sześciokątnych płatkach śniegu, ponownie odkrył ciąg Fibonacciego i zgadł, że kolejne proporcje  czyli stosunki
czyli stosunki 
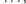 bardzo szybko, choć raz z lewej, raz z prawej strony, zbliżają się do wartości
bardzo szybko, choć raz z lewej, raz z prawej strony, zbliżają się do wartości 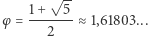 Liczba ta, zwana złotą proporcją, od Starożytności była wykorzystywana w sztuce, zwłaszcza w architekturze jako "reguła piękna" - wielkości, których stosunek jest równy
Liczba ta, zwana złotą proporcją, od Starożytności była wykorzystywana w sztuce, zwłaszcza w architekturze jako "reguła piękna" - wielkości, których stosunek jest równy  mają się wyróżniać przyjemną estetyką.
mają się wyróżniać przyjemną estetyką.

Gdy wiemy, że w przedziale domkniętym na prostej euklidesowej  każdy ciąg spełniający warunek Cauchy'ego jest zbieżny, to spostrzeżenie Keplera możemy uzasadnić w oparciu o twierdzenie Stefana Banacha o punkcie stałym z 1922 roku.
każdy ciąg spełniający warunek Cauchy'ego jest zbieżny, to spostrzeżenie Keplera możemy uzasadnić w oparciu o twierdzenie Stefana Banacha o punkcie stałym z 1922 roku.
Twierdzenie. Niech ![|T [a,b] [a,b]](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/2x-dc6090ae11f03f59c836b1d61ba50ea22e6664eb-im-33,33,33-FF,FF,FF.gif) silnie zbliża każdą parę punktów
silnie zbliża każdą parę punktów 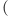 istnieje
istnieje  że
że 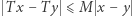 dla wszystkich
dla wszystkich ![|x,y ∈[a,b]).](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/6x-dc6090ae11f03f59c836b1d61ba50ea22e6664eb-im-33,33,33-FF,FF,FF.gif) Wtedy istnieje dokładnie jeden taki punkt
Wtedy istnieje dokładnie jeden taki punkt ![|u∈ [a,b],](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/7x-dc6090ae11f03f59c836b1d61ba50ea22e6664eb-im-33,33,33-FF,FF,FF.gif) że
że 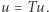
Uzasadnienie jest łatwe. Gdyby  to otrzymamy sprzeczność,
to otrzymamy sprzeczność,
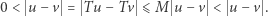 |
Zatem jeśli punkt stały istnieje, to dokładnie jeden. Weźmy dowolne ![|x0∈ [a,b]](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/3x-b7f6e6f82a63d2f121387fa74550f51685a0d6c3-im-33,33,33-FF,FF,FF.gif) i utwórzmy ciąg
i utwórzmy ciąg 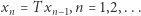 Wówczas
Wówczas

Ponieważ

więc
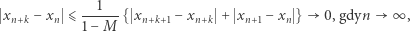 |
a to oznacza, że 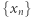 jest ciągiem Cauchy'ego i
jest ciągiem Cauchy'ego i ![x u∈ [a,b]. n](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/4x-715420191e95a27dcd3692413cdc18e090ef6164-im-33,33,33-FF,FF,FF.gif) Warunek
Warunek  oraz ciągłość przekształcenia
oraz ciągłość przekształcenia 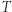 zapewniają, że
zapewniają, że 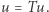
Zastosowanie.
Z warunku  dla
dla 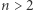 mamy
mamy
 |
Zależność tę możemy zapisać w postaci
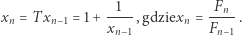 |
Zauważmy, że dla funkcji ![3- 3- T [2 ,2] [2 ,2]](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/1x-a3fa293224ff3f4e3cd21b25c9240c7c9d7877a1-im-33,33,33-FF,FF,FF.gif) danej wzorem
danej wzorem 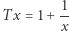 mamy
mamy
![1 1 1 4 3 T x− Ty = -−- =--- x − y ⩽- x −y ,gdyx, y∈ [-,2]. x y xy 9 2](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/3x-a3fa293224ff3f4e3cd21b25c9240c7c9d7877a1-dm-33,33,33-FF,FF,FF.gif) |
Zatem z twierdzenia Banacha ciąg 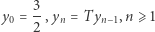 jest zbieżny do wartości
jest zbieżny do wartości 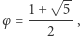 która jest pierwiastkiem równania
która jest pierwiastkiem równania  w przedziale
w przedziale ![3- [2 ,2].](/math/temat/matematyka/teoria_liczb/2020/05/31/fibonacci-spotyka-banacha/7x-a3fa293224ff3f4e3cd21b25c9240c7c9d7877a1-im-33,33,33-FF,FF,FF.gif) Ponieważ
Ponieważ  więc
więc 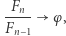 gdy
gdy 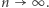
Opisana metoda (gdy trafnie dobierzemy zakres działania odpowiedniego przekształcenia 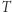 ) jest skuteczna w badaniu granicznych zachowań takich ilorazów również dla innych przedstawicieli z rodziny ciągów Fibonacciego.
) jest skuteczna w badaniu granicznych zachowań takich ilorazów również dla innych przedstawicieli z rodziny ciągów Fibonacciego.
Dobre bajki nigdy się nie kończą...