Dyskretny Darboux
Każda funkcja ciągła określona na zbiorze liczb rzeczywistych ma własność Darboux, tzn. jeśli dla pewnych 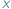 i
i 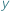 mamy
mamy 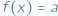 i
i 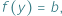 to w przedziale
to w przedziale 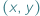 są przyjmowane wszystkie wartości między
są przyjmowane wszystkie wartości między  i
i 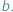 Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...
Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...
Rozważmy bowiem taką funkcję 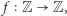 że
że 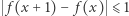 dla każdego
dla każdego 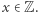 Ma ona własność analogiczną do wcześniej opisanej własności Darboux, tzn. jeśli dla pewnych
Ma ona własność analogiczną do wcześniej opisanej własności Darboux, tzn. jeśli dla pewnych 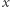 i
i 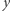 mamy
mamy 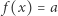 i
i 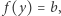 to na zbiorze
to na zbiorze 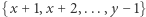 są przyjmowane wszystkie całkowite wartości między
są przyjmowane wszystkie całkowite wartości między 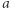 i
i 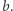 Spróbujmy zobaczyć na przykładach, jak potężna może być powyższa obserwacja.
Spróbujmy zobaczyć na przykładach, jak potężna może być powyższa obserwacja.
Metoda rozwiązania kolejnego zadania będzie nieznacznie różniła się od poprzednich, gdyż tym razem nasza funkcja będzie skakała o 2, ale tylko po liczbach parzystych.
Na koniec proponujemy Czytelnikom dwa zadania do samodzielnego rozwiązania.